url: https://hpc-tutorials.llnl.gov/mpi/virtual_topologies/

Virtual Topologies 虚拟拓扑

What Are They?

在MPI范畴内，虚拟拓扑描述了将MPI进程映射/排列到某种几何"形状"中的方式。

MPI支持的两类主要拓扑结构是笛卡尔拓扑（网格状）和图拓扑。

MPI拓扑是虚拟的——并行计算机的物理结构与进程拓扑之间可能不存在直接关联。

虚拟拓扑建立在MPI通信器和群组的基础之上。

这些拓扑必须由应用程序开发者通过编程方式构建。

Why Use Them?

Convenience

虚拟拓扑适用于具有特定通信模式的应用场景——即那些与MPI拓扑结构相匹配的通信模式。例如，对于需要基于网格数据进行四向最近邻通信的应用程序而言，笛卡尔拓扑会显得尤为便利。

Communication Efficiency

某些硬件架构可能会对跨节点通信带来性能损耗。

特定的MPI实现可以基于给定并行机器的物理特性来优化进程映射策略。

进程在MPI虚拟拓扑中的映射方式取决于具体的MPI实现，且这种映射机制有可能被完全忽略。

Example:

下图展示了将进程映射至笛卡尔虚拟拓扑的简化示意图：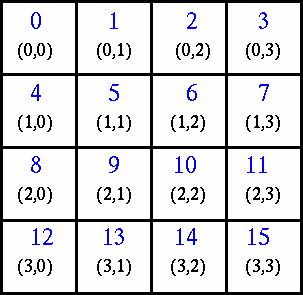

Code examples

基于16个处理器创建一个4×4的笛卡尔拓扑，并让每个进程与其四个相邻进程交换各自的排名值。

#include "mpi.h"
#include <stdio.h>

#define SIZE 16        // 总进程数，4x4网格
#define UP    0        // 上方向索引
#define DOWN  1        // 下方向索引  
#define LEFT  2        // 左方向索引
#define RIGHT 3        // 右方向索引

int main(int argc, char *argv[]) {
    int numtasks, rank, source, dest, outbuf, i, tag=1,
        // 初始化接收缓冲区，MPI_PROC_NULL表示空进程（用于边界处理）
        inbuf[4]={MPI_PROC_NULL,MPI_PROC_NULL,MPI_PROC_NULL,MPI_PROC_NULL,},
        nbrs[4],           // 存储四个方向的邻居进程rank
        dims[2]={4,4},     // 定义2维网格尺寸：4x4
        periods[2]={0,0},  // 网格周期边界：0表示非周期性
        reorder=0,         // 是否允许MPI重新排列进程rank
        coords[2];         // 存储当前进程在网格中的坐标

    MPI_Request reqs[8];   // 非阻塞通信请求数组（4个发送+4个接收）
    MPI_Status stats[8];   // 通信状态数组
    MPI_Comm cartcomm;     // 笛卡尔通信域

    // 初始化MPI环境
    MPI_Init(&argc,&argv);
    // 获取总进程数
    MPI_Comm_size(MPI_COMM_WORLD, &numtasks);

    // 检查进程数是否符合要求（必须是16个）
    if (numtasks == SIZE) {
        // 创建2维笛卡尔网格拓扑
        MPI_Cart_create(MPI_COMM_WORLD, 2, dims, periods, reorder, &cartcomm);
        // 在笛卡尔拓扑中获取当前进程rank
        MPI_Comm_rank(cartcomm, &rank);
        // 获取当前进程在网格中的坐标
        MPI_Cart_coords(cartcomm, rank, 2, coords);
        
        // 在维度0（y轴）上计算上下邻居
        MPI_Cart_shift(cartcomm, 0, 1, &nbrs[UP], &nbrs[DOWN]);
        // 在维度1（x轴）上计算左右邻居  
        MPI_Cart_shift(cartcomm, 1, 1, &nbrs[LEFT], &nbrs[RIGHT]);

        // 打印进程信息
        printf("rank= %d coords= %d %d  neighbors(u,d,l,r)= %d %d %d %d\n",
                rank,coords[0],coords[1],nbrs[UP],nbrs[DOWN],nbrs[LEFT],
                nbrs[RIGHT]);

        outbuf = rank;  // 要发送的数据：当前进程rank

        // 与四个邻居进行非阻塞通信
        for (i=0; i<4; i++) {
            dest = nbrs[i];    // 目标邻居
            source = nbrs[i];  // 源邻居
            
            // 非阻塞发送：向邻居发送当前rank
            MPI_Isend(&outbuf, 1, MPI_INT, dest, tag,
                    MPI_COMM_WORLD, &reqs[i]);
            // 非阻塞接收：从邻居接收数据
            MPI_Irecv(&inbuf[i], 1, MPI_INT, source, tag,
                    MPI_COMM_WORLD, &reqs[i+4]);
        }

        // 等待所有8个通信操作完成（4个发送+4个接收）
        MPI_Waitall(8, reqs, stats);

        // 打印接收到的邻居数据
        printf("rank= %d                  inbuf(u,d,l,r)= %d %d %d %d\n",
                rank,inbuf[UP],inbuf[DOWN],inbuf[LEFT],inbuf[RIGHT]);  
    }
    else {
        // 进程数不符合要求时的错误信息
        printf("Must specify %d processors. Terminating.\n",SIZE);
    }

    // 终止MPI环境
    MPI_Finalize();
}

下面是编译运行命令：

mpicc test.c -o test
mpirun --oversubscribe -np 16 ./test # 如果电脑核心数不够，要加 --oversubscribe

预期输出：

rank= 13 coords= 3 1  neighbors(u,d,l,r)= 9 -2 12 14
rank= 13                  inbuf(u,d,l,r)= 9 -2 12 14
rank= 14 coords= 3 2  neighbors(u,d,l,r)= 10 -2 13 15
rank= 14                  inbuf(u,d,l,r)= 10 -2 13 15
rank= 15 coords= 3 3  neighbors(u,d,l,r)= 11 -2 14 -2
rank= 15                  inbuf(u,d,l,r)= 11 -2 14 -2
rank= 0 coords= 0 0  neighbors(u,d,l,r)= -2 4 -2 1
rank= 0                  inbuf(u,d,l,r)= -2 4 -2 1
rank= 1 coords= 0 1  neighbors(u,d,l,r)= -2 5 0 2
rank= 1                  inbuf(u,d,l,r)= -2 5 0 2
rank= 2 coords= 0 2  neighbors(u,d,l,r)= -2 6 1 3
rank= 2                  inbuf(u,d,l,r)= -2 6 1 3
rank= 3 coords= 0 3  neighbors(u,d,l,r)= -2 7 2 -2
rank= 3                  inbuf(u,d,l,r)= -2 7 2 -2
rank= 4 coords= 1 0  neighbors(u,d,l,r)= 0 8 -2 5
rank= 4                  inbuf(u,d,l,r)= 0 8 -2 5
rank= 5 coords= 1 1  neighbors(u,d,l,r)= 1 9 4 6
rank= 5                  inbuf(u,d,l,r)= 1 9 4 6
rank= 6 coords= 1 2  neighbors(u,d,l,r)= 2 10 5 7
rank= 6                  inbuf(u,d,l,r)= 2 10 5 7
rank= 7 coords= 1 3  neighbors(u,d,l,r)= 3 11 6 -2
rank= 7                  inbuf(u,d,l,r)= 3 11 6 -2
rank= 8 coords= 2 0  neighbors(u,d,l,r)= 4 12 -2 9
rank= 8                  inbuf(u,d,l,r)= 4 12 -2 9
rank= 9 coords= 2 1  neighbors(u,d,l,r)= 5 13 8 10
rank= 9                  inbuf(u,d,l,r)= 5 13 8 10
rank= 10 coords= 2 2  neighbors(u,d,l,r)= 6 14 9 11
rank= 10                  inbuf(u,d,l,r)= 6 14 9 11
rank= 11 coords= 2 3  neighbors(u,d,l,r)= 7 15 10 -2
rank= 11                  inbuf(u,d,l,r)= 7 15 10 -2
rank= 12 coords= 3 0  neighbors(u,d,l,r)= 8 -2 -2 13
rank= 12                  inbuf(u,d,l,r)= 8 -2 -2 13