Python复习&&PyTorch简单线性回归

学习目标

通过本课程，学员将学习到python类的相关知识，掌握类的创建初始化，类的属性和方法，熟悉制作python包的操作步骤，并将其发布到PyPi。同时，学员也将学会使用Pytorch进行简单线性回归模型的训练与评估，熟练掌握在昇腾硬件设备上开发验证的技巧。

相关知识点

• Python复习&&PyTorch简单线性回归

学习内容

1 Python复习&&PyTorch简单线性回归

在Python中，类是一种用于创建对象的蓝图或者模板。它定义了对象的属性（数据）和方法（行为）。类是面向对象编程（OOP）的核心概念，它让代码具备模块化、可复用性以及可扩展性。
属性是类的变量，用于存储对象的数据。属性可分为实例属性和类属性。
实例属性：每个对象独有的属性，在实例化对象时进行初始化。通常在 init 方法里定义。
类属性：由类的所有实例共享的属性，定义在类内部但在方法外部。
方法是类的函数，用来定义对象的行为。

1.1 类和函数

我们将实现两个用于统计分布的类及其方法来调用 Python 类和函数。之后，我们会将它们包装在一个包中，并将其发布到PyPi，这是存储所有Python包的官方 Python存储库。

1.1.1 通用Distribution类

该类是用于计算和可视化概率分布的泛型分布类。它具有以下属性：

• mean（float）：表示分布的平均值，默认值 = 0。
• stdev（float）：表示分布的标准差，默认值 = 1。
• data（浮点数列表）：从数据文件中提取的浮点数列表。

创建类并且初始化。

class Distribution:
	def __init__(self, mu=0, sigma=1):
		self.mean = mu
		self.stdev = sigma
		self.data = []

• __init__是类的构造函数，它初始化类的属性，mean, stdev, data。

def read_data_file(self, file_name):	
	with open(file_name) as file:
		data_list = []
		line = file.readline()
		while line:
			data_list.append(int(line))
			line = file.readline()
	file.close()
	self.data = data_list

该方法用于从文本文件中读取数据。文本文件每行应有一个数字 （float）。数字存储在类的属性中。file_name参数是要从中读取的文件的名称。

该方法使用函数打开文件，并逐行读取文件。使用函数将每行转换为整数并附加到列表中。最后，为该属性分配值 。

1.1.2 Gaussian类

Gaussian类是Distribution类的子类。它表示高斯分布，并提供计算和可视化分布的方法。
它具有以下属性:

• mean (float): 表示分布的平均值。
• stdev (float): 表示分布的标准差。
• data_list (浮点数列表): 从数据文件中提取的浮点数列表。

他们是Distribution类的属性，Gaussian类可以继承这些属性。

class Gaussian(Distribution):
	def __init__(self, mu=0, sigma=1):
		Distribution.__init__(self, mu, sigma)

init(self, mu=0, sigma=1)使用指定的平均值和标准差初始化对象。它调用类的方法以初始化 mean、standard deviation 和 data 属性。

它具有以下方法：

• 计算平均值：计算数据集的平均值。它将平均值作为浮点数返回。

def calculate_mean(self):			
	avg = 1.0 * sum(self.data) / len(self.data)
	self.mean = avg
	return self.mean

• 计算标准差：计算数据集的标准差。该参数指示数据是表示样本还是总体。它将标准差作为浮点数返回。

def calculate_stdev(self, sample=True):
	if sample:
		n = len(self.data) - 1
	else:
		n = len(self.data)
	mean = self.calculate_mean()
	sigma = 0
	for d in self.data:
		sigma += (d - mean) ** 2
	sigma = math.sqrt(sigma / n)
	self.stdev = sigma
	return self.stdev

• 绘制直方图：使用matplotlib库输出实例变量数据的直方图。

def plot_histogram(self):
	plt.hist(self.data)
	plt.title('Histogram of Data')
	plt.xlabel('data')
	plt.ylabel('count')

• 分布相加：将两个高斯分布相加。参数为 instance。它返回一个新的分布，其平均值和标准差是根据两个分布的总和计算得出的。

def __add__(self, other):
	result = Gaussian()
	result.mean = self.mean + other.mean
	result.stdev = math.sqrt(self.stdev ** 2 + other.stdev ** 2)
	return result

• 计算概率密度函数：计算指定点处高斯分布的概率密度函数(PDF)。它将PDF值作为浮点数返回。

def pdf(self, x):
	return (1.0 / (self.stdev * math.sqrt(2*math.pi))) * math.exp(-0.5*((x - self.mean) / self.stdev) ** 2)

• 归一化处理：沿同一范围绘制数据的归一化直方图和概率密度函数(PDF)。该参数指定数据点的数量。它将PDF图的x和y值作为列表返回。

def plot_histogram_pdf(self, n_spaces = 50):
	mu = self.mean
	sigma = self.stdev
	min_range = min(self.data)
	max_range = max(self.data)
	 # calculates the interval between x values
	interval = 1.0 * (max_range - min_range) / n_spaces
	x = []
	y = []
	# calculate the x values to visualize
	for i in range(n_spaces):
		tmp = min_range + interval*i
		x.append(tmp)
		y.append(self.pdf(tmp))
	# make the plots
	fig, axes = plt.subplots(2,sharex=True)
	fig.subplots_adjust(hspace=.5)
	axes[0].hist(self.data, density=True)
	axes[0].set_title('Normed Histogram of Data')
	axes[0].set_ylabel('Density')
	axes[1].plot(x, y)
	axes[1].set_title('Normal Distribution for \n Sample Mean and Sample Standard Deviation')
	axes[0].set_ylabel('Density')
	plt.show()

	return x, y

1.2 制作python包并发布到PyPI

制作python包步骤：

• 创建项目目录：首先为项目创建一个新目录。这将用作 Python 包的根目录。

• 设置包结构：在项目目录中，使用包的名称创建一个新目录。此目录将包含包的源代码。

接下来，在 package 目录中创建一个名为__init__.py的文件。将目录标记为 Python 包时需要此文件。该文件在导入包时执行，可用于定义变量、导入模块或执行包所需的任何其他初始化任务。

• 编写软件包代码： 在 package 目录中，编写软件包的代码。这可以包括模块、类、函数等。以对包有意义的方式组织代码。

• 创建setup.py文件：在项目目录中，创建一个名为setup.py文件，此文件用于定义包的元数据和依赖项。项目目录应如图1所示，其中包含前面单元格中每个类的代码：

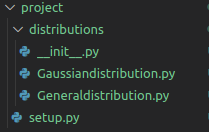
图1：项目目录

• 修改setup.py文件：打开setup.py并定义包元数据和依赖项。下面是一个示例。

  from setuptools import setup
  setup(
  	name='your-package-name',
  	version='1.0.0',
  	description='A short description of your package',
  	author='Your Name',
  	author_email='your-email@example.com',
  	url='https://github.com/your-username/your-package-repo',
  	packages=['your_package_name'],
  	install_requires=[
  		'dependency1',
  		'dependency2',
  	],
  )
  

• 创建账户：在PyPi上创建账户。

• 终端运行：打开 powershell 或终端，将目录更改为项目目录，然后运行这些命令。

	python3 -m pip install --user --upgrade setuptools wheel
	python3 setup.py sdist bdist_wheel
	python3 -m pip install --user --upgrade twine
	twine upload dist/*

系统会提示输入用户名和密码。

• 软件包安装：尝试使用此命令在任何位置安装软件包。

	pip install packageName

1.3 PyTorch简单线性回归

使用PyTorch实现简单线性回归，包括定义模型、损失函数和优化器，以及训练模型。
线性回归是一种用于建立自变量和因变量之间线性关系的统计模型。简单线性回归只有一个自变量和一个因变量。

损失函数用于衡量模型预测值与真实值之间的差异。在简单线性回归中，常用的损失函数是均方误差（Mean Squared Error, MSE）。

优化器的作用是通过调整模型的参数（权重和偏置）来最小化损失函数。在PyTorch中，随机梯度下降（Stochastic Gradient Descent, SGD）是一种常用的优化算法。

模型训练过程通常包含以下步骤：

• 定义模型：构建一个线性回归模型。
• 定义损失函数：选择合适的损失函数，如 MSE。
• 定义优化器：选择合适的优化器，如 SGD。
• 迭代训练：多次迭代，每次迭代中进行前向传播、计算损失、反向传播和参数更新。

1.3.1 定义模型并训练

安装依赖。

%pip install torch==2.2.0 torch_npu==2.2.0

import torch
import torch.nn as nn
import torch.optim as optim

# Define the input data
x = torch.tensor([[1.0], [2.0], [3.0], [4.0], [5.0], [6.0], [7.0], [8.0], [9.0], [10.0]])
y = torch.tensor([[2.0], [4.0], [6.0], [8.0], [10.0], [12.0], [14.0], [16.0], [18.0], [20.0]])

# 定义linear regression model
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)  # 1 input feature, 1 output feature

    def forward(self, x):
        return self.linear(x)

model = LinearRegression()

# 定义损失函数和优化器
criterion = nn.MSELoss() #mean squared error loss
optimizer = optim.SGD(model.parameters(), lr=0.01) #stochastic gradient descent

# 训练模型
num_epochs = 10
for epoch in range(num_epochs):
    # Forward pass
    outputs = model(x)
    loss = criterion(outputs, y)

    # Backward and optimize
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    print(f"Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item()}")

1.3.2 评估模型

import matplotlib.pyplot as plt
# Test the model
test_input = torch.tensor([[4.0]])
predicted_output = model(test_input)
print(f"Predicted output for input 4: {predicted_output.item()}")

# Plot the actual output
plt.scatter(x, y, color='blue', label='Actual')

# Plot the predicted output
plt.scatter(x, model(x).detach().numpy(), color='red', label='Predicted', marker='x')
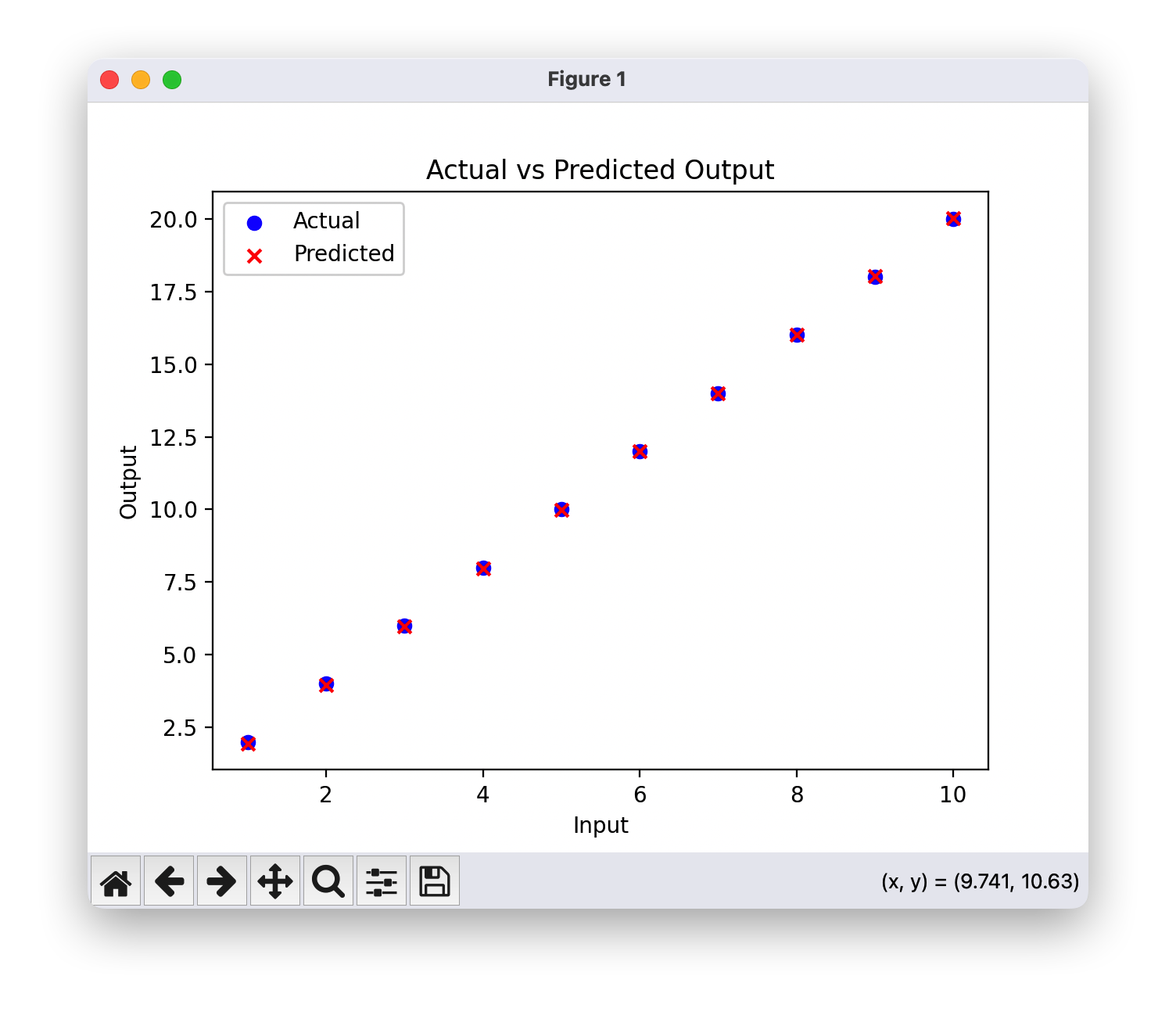
plt.title('Actual vs Predicted Output')

# Add labels and legend
plt.xlabel('Input')
plt.ylabel('Output')
plt.legend()

# Show the plot
plt.show()