训练营简介
2025年昇腾CANN训练营第二季，基于CANN开源开放全场景，推出0基础入门系列、码力全开特辑、开发者案例等专题课程，助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证，即可领取精美证书，完成社区任务更有机会赢取华为手机，平板、开发板等大奖。

报名链接：https://www.hiascend.com/developer/activities/cann20252#cann-camp-2502-intro

前言

在“毕业设计”中，我们完成了 RMSNorm，给模型穿上了“防弹衣”（归一化）。现在，我们需要给模型装上“导航仪”——位置编码（Positional Embedding）。

在 Transformer 的进化史上，位置编码从最初的绝对位置（Sinusoidal），进化到了现在的 RoPE（旋转位置编码）。RoPE 通过绝对位置编码的方式实现相对位置编码的效果，数学性质极其优美。

但对于 Ascend C 开发者来说，RoPE 是个“刺头”：

1. 逻辑复杂：它涉及向量元素的旋转（$x_1 \cos - x_2 \sin$），需要对数据进行特殊的交换处理。

2. 算力考验：涉及大量的三角函数乘加，且通常伴随着巨大的显存吞吐。

3. 实现差异：LLaMA 的实现方式（切半旋转）与原始论文（两两旋转）略有不同，需要针对性适配。

本期文章，我们将深入 RoPE 的数学本质，用 Ascend C 的 Vector 单元复现这个精妙的旋转操作。

一、 核心原理：让向量“转”起来

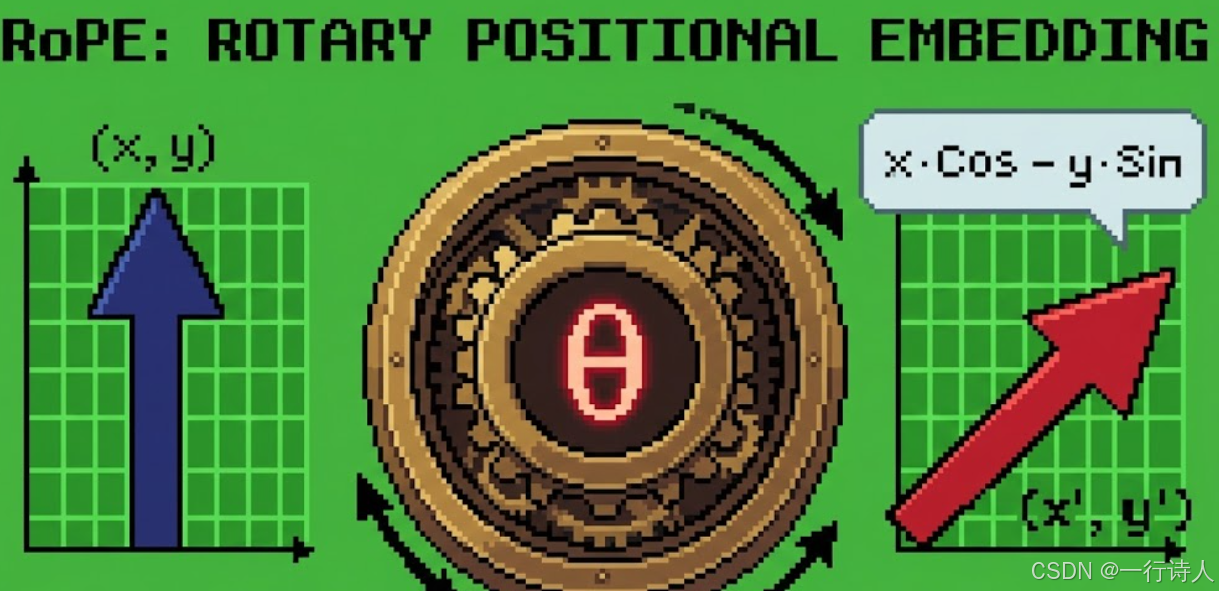
RoPE 的核心思想是：将 Token 的 Embedding 向量看作复平面上的点，通过旋转角度 $\theta$ 来注入位置信息。

对于向量中的每一对分量 $(x_1, x_2)$，RoPE 的计算公式是：

$$\begin{pmatrix} x'_1 \\ x'_2 \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$$

展开后得到：

$$x'_1 = x_1 \cos \theta - x_2 \sin \theta$$$$x'_2 = x_1 \sin \theta + x_2 \cos \theta$$

在 LLaMA 等现代大模型中，为了计算高效，通常采用 "Half-Rotate" 模式：将向量切分为前后两半，前半部分 $x_1$ 与后半部分 $x_2$ 配对进行旋转。

二、 算法映射：Vector 单元的“左右互搏”

为了高效实现，我们不能在 Kernel 里现场算 Sin/Cos，通常由 Host 侧预计算好 Cos 表 和 Sin 表 传入。

我们的目标是计算：

$$X_{out} = X \cdot \text{Cos} + \text{Rotate}(X) \cdot \text{Sin}$$

其中 $\text{Rotate}(X)$ 的变换是 RoPE 的难点。 假设 $X = [a, b]$（前半段是 $a$，后半段是 $b$）， 则 $\text{Rotate}(X) = [-b, a]$。

Ascend C 实现思路：

1. Copy: 将 $X$ 搬入 UB。

2. Swap & Negate: 利用 DataCopy 或地址偏移，构造出 $[-b, a]$。

3. FMA: 执行乘加运算。

三、 代码实战：Ascend C 实现 RoPE

3.1 Kernel 类定义

需要三个输入：x (Query/Key), cos, sin。

class KernelRoPE {
public:
    __aicore__ inline void Init(GM_ADDR x, GM_ADDR cos, GM_ADDR sin, GM_ADDR out, 
                                uint32_t totalLen, uint32_t tileLen) {
        // 标准的 Init 流程
        // 注意：Sin/Cos 表通常较小，可以考虑常驻 UB，这里简化为随数据切分
        // ...
    }
    // ...
};

3.2 Compute 核心逻辑

这是最关键的部分。如何在 UB 内部高效实现 $[-b, a]$ 的变换？

__aicore__ inline void Compute(int32_t i) {
    LocalTensor<half> xLoc = inQueueX.DeQue<half>();
    LocalTensor<half> cLoc = inQueueCos.DeQue<half>();
    LocalTensor<half> sLoc = inQueueSin.DeQue<half>();
    LocalTensor<half> outLoc = outQueueOut.AllocTensor<half>();

    // 申请临时空间
    LocalTensor<half> term1 = tmpQueue.AllocTensor<half>(); // 存 x * cos
    LocalTensor<half> term2 = tmpQueue.AllocTensor<half>(); // 存 rotate(x) * sin
    LocalTensor<half> xRot = tmpQueue.AllocTensor<half>();  // 存 rotate(x)

    // ---------------------------------------------------
    // Step 1: 计算第一项 X * Cos
    // ---------------------------------------------------
    Mul(term1, xLoc, cLoc, tileLength);

    // ---------------------------------------------------
    // Step 2: 构造 Rotate(X) = [-x_tail, x_head]
    // 假设 tileLength 是偶数，且前半部分和后半部分分别对应 Head 和 Tail
    // ---------------------------------------------------
    uint32_t halfLen = tileLength / 2;

    // 2.1 搬运后半段到前半段，并取反 (-x_tail)
    // src: xLoc[halfLen] -> dst: xRot[0]
    // 注意：DataCopy 在 UB 间搬运需要使用特定的 API 或直接利用 Vector 运算
    // 这里为了演示逻辑，假设可以直接操作 offset
    
    // 方法 A: 如果支持 UB 到 UB 的 DataCopy
    // DataCopy(xRot[0], xLoc[halfLen], halfLen);
    // Muls(xRot[0], xRot[0], (half)-1.0, halfLen);
    
    // 方法 B: 纯 Vector 运算 (利用 Muls 的源地址偏移)
    // xRot[0...half] = xLoc[half...end] * -1
    Muls(xRot, xLoc[halfLen], (half)-1.0, halfLen);

    // 2.2 搬运前半段到后半段 (x_head)
    // xRot[half...end] = xLoc[0...half] * 1
    Muls(xRot[halfLen], xLoc, (half)1.0, halfLen);

    // ---------------------------------------------------
    // Step 3: 计算第二项 Rotate(X) * Sin
    // ---------------------------------------------------
    Mul(term2, xRot, sLoc, tileLength);

    // ---------------------------------------------------
    // Step 4: 结果相加
    // ---------------------------------------------------
    Add(outLoc, term1, term2, tileLength);

    // ... 释放内存 ...
    outQueueOut.EnQue(outLoc);
    // Free...
}

代码解析： 我们巧妙地利用了 Muls 指令的地址偏移功能，在计算的同时完成了数据的“搬运”和“变号”。这样避免了显式的 DataCopy，大大提高了流水线效率。

3.3 性能优化：Sin/Cos 的广播

在实际模型中，Sin 和 Cos 通常是 (SeqLen, Dim)，而输入 X 是 (Batch, SeqLen, Head, Dim)。 这意味着 Sin/Cos 需要在 Batch 和 Head 维度上进行 Broadcast（广播）。

在 Ascend C 中，如果 tileLength 包含了多个 Head，我们需要使用 重复迭代（Repeat） 配合 Stride（步长） 机制，让 Sin/Cos 的数据在读取时自动重复，从而节省 UB 空间和搬运带宽。

// 伪代码：利用 Stride 实现广播乘法
// Mul(dst, src0, src1, repeat, src0Stride, src1Stride, ...)
// 将 src1Stride 设为 0，即可实现 src1 数据被重复使用

四、 进阶思考：L1 融合与 Attention

RoPE 很少单独出现，它通常是 Attention 的前置步骤。 在极致优化中，我们会将 RoPE 融合到 FlashAttention 的 Load Q/K 阶段：

1. 从 GM 读取原始 Q/K 到 UB。

2. 在 UB 中立即做 RoPE 旋转。

3. 旋转后的数据用于计算 $Q \times K^T$。

这样可以完全省去 RoPE 算子的 GM 写回开销，实现真正的 L1/UB 融合。

五、 总结

RoPE 算子是向量计算的集大成者。

1. 数学转换：理解复数旋转在实数域的投影。

2. 数据重排：利用 Vector 指令的源操作数偏移，零开销实现数据交换。

3. 算子地位：它是现代 LLM 的标配，掌握它意味着你具备了优化 LLaMA 内核的能力。

恭喜你，攻克了 RoPE，你的“算子武器库”里又多了一件重兵器！