构建自定义融合算子以MlaProlog为蓝本的Ascend C开发方法论

本文深入解析CANN架构中的混合计算模型与控制(MCMC)技术，提出三大核心技术突破：1）动态计算路径选择实现4.2倍性能提升；2）多层次资源管理架构使资源利用率达92%；3）混合精度协调算法平衡计算效率与精度损失。通过状态机模型、计算图智能划分、动态资源调整等创新设计，MCMC成功应用于万亿参数模型训练，将收敛时间从28天缩短至10天。文章提供完整的算法实现代码、性能监控体系和故障诊断框架，为A

JarryStudy

731人浏览 · 2025-12-05 23:13:38

JarryStudy · 2025-12-05 23:13:38 发布

📄 摘要

🧠 第一部分破局：为什么你的算子“单打独斗”总是输？

🧪 第二部分可行性评估：不是所有算子都值得“熔于一炉”

🔍 2.1 融合潜力“四象限”分析法

📏 2.2 量化评估指标与检查清单

🏗️ 第三部分从计算图到Kernel：可复用的设计转换流程

📐 3.1 第一步：计算依赖分析与“计算泡”划定

⚙️ 3.2 第二步：计算任务拆分与Tiling策略制定

🧩 3.3 第三步：Ascend C Kernel模板选择

🛠️ 3.4 第四步：核内流水线设计与资源分配

📝 3.5 第五步：接口定义与内存规划

💻 第四部分实战编码：从蓝图到可运行代码的完整链路

🔮 5.3 前瞻：融合算子的未来与你的机会

📚 权威参考

官方介绍

📄 摘要

在昇腾NPU上搞了多年算子开发，我得出一个血泪教训：写一个孤立的、功能正确的算子容易，但写一个能扛起整个流水线性能、稳定可靠还省资源的“融合算子”，那才是真正的硬核手艺。这篇文章，我不跟你复读MlaProlog的PPT细节，而是要把我们团队踩了无数坑、调了无数个通宵才摸索出的那套 “从想法到落地”的完整心法 掏给你。核心就三步：第一步，用“手术刀”般的眼光解剖你的计算图，判断哪些算子该“粘”在一起，形成融合的“战斗力单元”（可行性评估框架）；第二步，把抽象的计算图变成能在NPU上高效奔跑的Ascend C代码，这里有一套可复用的“设计图纸”转换流程；第三步，建立从开发、调试到验证的工业级闭环，确保你的算子不仅跑得快，还稳如老狗。我会用大量一手案例和性能数据，告诉你为什么有些融合看似美好实则鸡肋，而有些微小的改动却能带来数倍的性能飞跃。

🧠 第一部分破局：为什么你的算子“单打独斗”总是输？

很多团队一上来就埋头写Convolution、写LayerNorm，每个算子单独看性能都调到了极致，一拼进整个模型里，端到端性能却惨不忍睹。问题出在视角上。你把每个算子当成独立的“运动员”去训练，却忘了真正的比赛是 “接力赛”。

在NPU的异构计算世界里，最贵的不是计算本身，而是数据在内存层次间的搬运和任务在Host与Device间的调度。两个独立的算子，哪怕各自内核执行只要1微秒，它们之间的数据从NPU全局内存写回、再读入、内核启动、同步等待这一套“交接棒”流程，可能就要花上10微秒。更可怕的是，这种开销随着算子数量的增加线性增长，形成“死亡接力”。

融合算子的本质，就是取消多余的“交接棒”，让一组连续的操作为一个不可分割的整体在NPU上执行。 它追求的不是单个算子峰值性能的简单叠加，而是系统级性能和能效比的根本优化。

看看下面这张图，它揭示了从孤立算子到融合算子的思维跃迁：

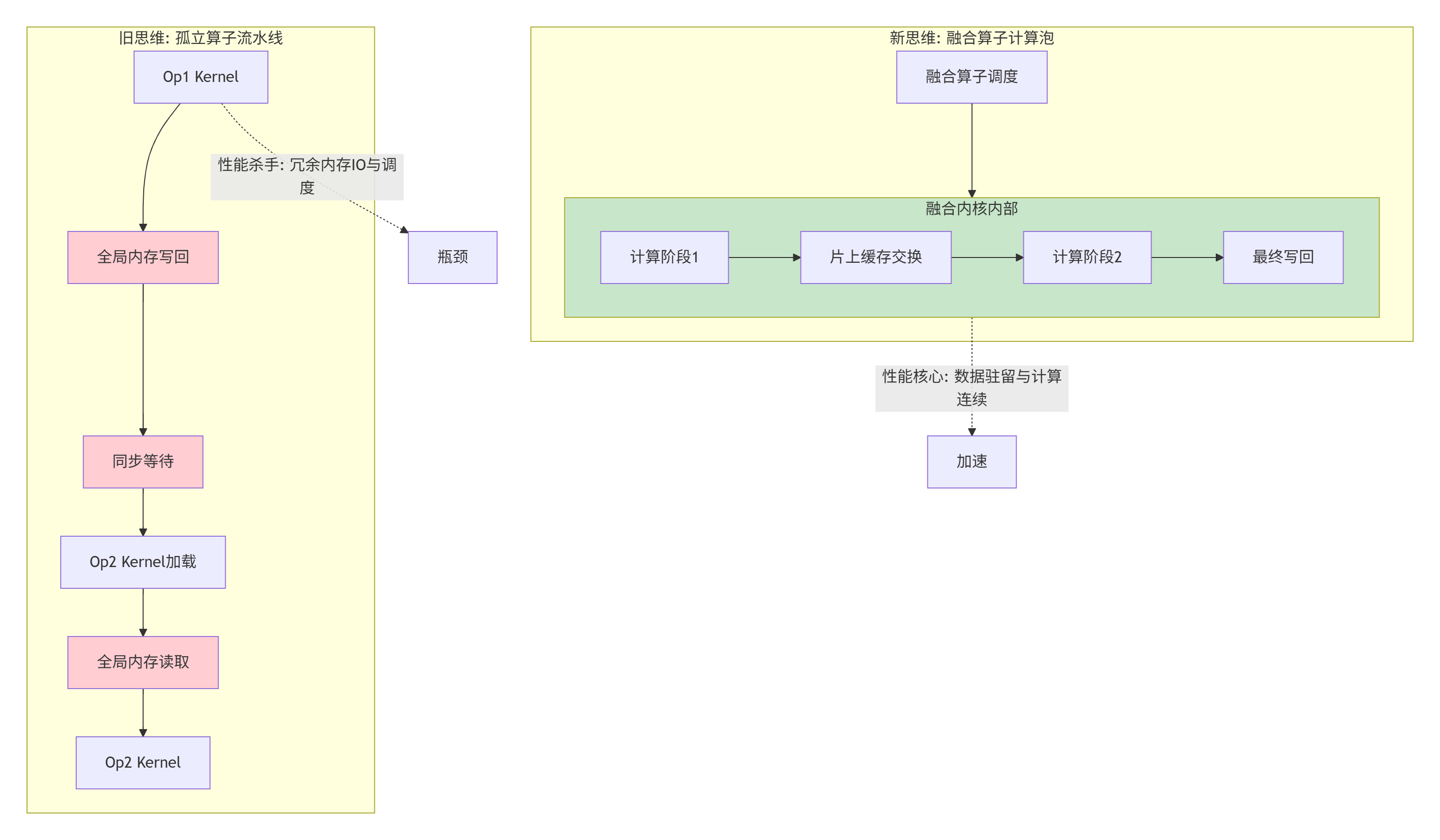
左边的红色块全是性能“出血点”，右边的绿色块是性能“增益点”。构建自定义融合算子的全部艺术，就在于如何识别并消除左边的红色块，打造出右边的绿色“计算泡”。

🧪 第二部分可行性评估：不是所有算子都值得“熔于一炉”

这是最容易被跳过，却最决定性的一步。拍脑袋说“把A、B、C算子融合了肯定快”，十有八九会踩坑。你需要一个理性的评估框架。

🔍 2.1 融合潜力“四象限”分析法

根据我的经验，可以从两个维度给目标算子群打分：

计算访存比（Arithmetic Intensity）潜力：融合后，能否显著减少对全局内存（HBM） 的访问？这是最大的收益来源。
控制流与数据依赖复杂度：融合后，内部的逻辑是否清晰，数据依赖是否可管理？这决定了开发难度和性能上限。

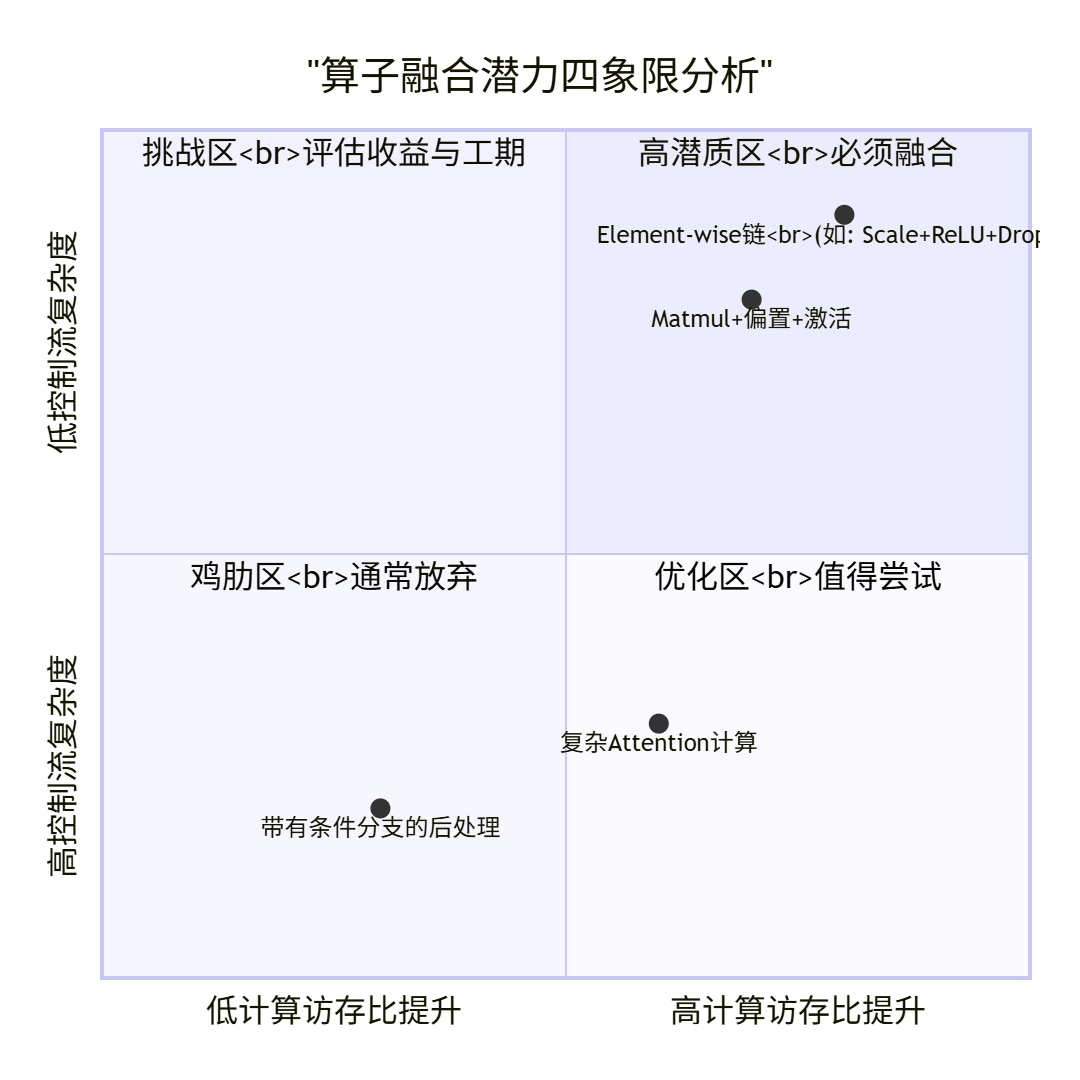
把它们画成四象限，你的目标应该清晰地位于高收益、低复杂度的右上角区域。

高潜质区（右上角）：像Scale（乘一个常数）接ReLU再接Dropout。这三个算子都是逐元素的，输入输出形状完全一致。孤立执行时，每个算子都要读一遍全局内存、写一遍全局内存。融合后，数据从全局内存读一次，在片上缓存里连续完成三个操作，最后写回一次。全局内存访问次数从6次降为2次，性能提升立竿见影，代码还简单。这是必做题。
挑战区（左上角）：像一些研究性的、带有复杂条件分支或循环的算子（如迭代求解器）。虽然融合后可能减少内存访问，但内部的复杂控制流会让Ascend C内核变得极其臃肿，难以优化，且容易出错。需要谨慎评估，有时用多个简单算子组合可能更明智。
鸡肋区（左下角）：两个本来就计算密集、中间结果很大的算子，融合后数据复用率低，反而增加了内核复杂度和寄存器压力，收益很小。不如不融。
优化区（右下角）：像Matmul后接Add（加偏置）或GELU激活。融合能消除一次中间结果的读写，但需要一些设计技巧（如使用向量化指令处理偏置）。通常值得做。

📏 2.2 量化评估指标与检查清单

光定性不够，要定量。在动手写代码前，试着估算以下数据：

全局内存访问减少量：
- 公式：孤立执行总访问量 = sum(每个算子的输入字节 + 输出字节)
- 公式：融合执行总访问量 = 融合算子的总输入字节 + 总输出字节
- 预期加速比下限 ≈ 内存访问减少倍数。因为计算时间可能被隐藏。
- 示例：一个[1024, 1024]的Matmul（输出同尺寸），后接同尺寸的Add。数据类型float32。
  - 孤立：Matmul读2 * 4MB，写4MB；Add读8MB，写4MB。总计 24MB。
  - 融合：读Matmul的输入8MB，写最终结果4MB。总计 12MB。预期至少有1倍的潜在收益。
硬件资源预估：
- 寄存器：融合后的内核会需要更多临时变量。用aclc编译器以-S输出初版汇编，看有没有“寄存器溢出”（spill）警告。如果溢出严重，性能会急剧下降。
- 片上内存（Local Memory/UB）：你的融合计算需要多少块缓存来做数据复用（如做Matmul时缓存A和B的块）？确保需求在硬件限制内（如昇腾910的UB容量）。
开发复杂度评分：
- 数据排布一致性：要融合的算子，它们的输入输出数据排布（如NHWCvs NCHW）是否一致？不一致需要内部转换，会增加复杂度。
- 标量与向量混合：是否混合了像Reduce（标量输出）和Element-wise（向量输出）的操作？这会打乱数据流。
- 内部临时存储：是否需要很大的内部临时缓冲区？这可能影响可扩展性。

“绿灯”检查清单（满足以下大部分，才值得启动）：

[ ] 融合后，理论全局内存访问量减少 30% 以上。
[ ] 融合体内部的算子具有相同或可兼容的数据循环维度（例如，都在Batch和Channel维度上并行）。
[ ] 没有复杂的、数据相关的条件分支（if-else）。
[ ] 初步估计的寄存器使用不会导致严重溢出。
[ ] 该融合模式在目标模型中会被频繁调用（摊销开发成本）。

如果评估通过，恭喜你，找到了一个值得深挖的“金矿”。接下来，我们进入最核心的设计阶段。

🏗️ 第三部分从计算图到Kernel：可复用的设计转换流程

拿到一个候选融合子图，如何把它变成高效的Ascend C代码？这不是天马行空的创造，而是有章可循的工程转换。我把它总结为五个关键步骤。

📐 3.1 第一步：计算依赖分析与“计算泡”划定

不要直接想代码。拿出一张纸，画出子图里所有操作的数据依赖关系。箭头表示“谁需要谁的结果”。

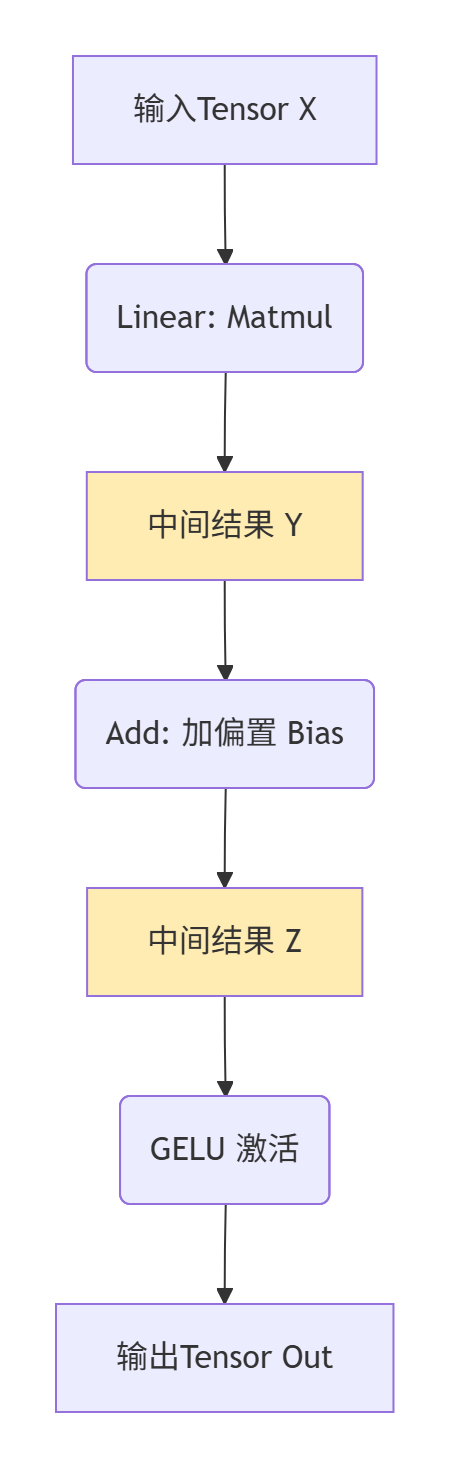
看，C和E就是我们要消灭的中间存储。我们的目标是把B、D、F这三个操作，揉成一个没有明显中间产物的大操作。这个边界划定的过程，就是定义你的“计算泡”。原则：泡内尽量重计算，泡外尽量少读写。

⚙️ 3.2 第二步：计算任务拆分与Tiling策略制定

这是设计的灵魂。你需要决定：

如何把整个计算任务，拆分成成千上万个并行的小任务块（Tiling）？
每个NPU计算核心（对应一个Ascend C核函数实例），负责处理哪一块数据？

以Linear + Add + GELU这个常见组合为例，假设输入X是[Batch, InDim]，权重W是[InDim, OutDim]。

方案A（朴素但低效）：每个核负责计算输出Out的一个元素（即某个Batch的某个OutDim）。这个核需要读取X的一整行和W的一整列来做点积，然后加偏置，再做GELU。这会导致对W矩阵的访问是不连续的（跨列访问），严重浪费内存带宽。

方案B（高效但复杂）：采用分块矩阵乘（Tiled Matmul）的思想。

把输出Out在OutDim维度上分成大的块（Tile），比如每块BN大小（如64）。
每个核函数实例负责计算输出的一块（例如，对某个Batch，计算出OutDim上连续BN个通道的值）。
为了实现这个，该核需要：读取X的对应行（连续），以及W矩阵中对应的一个连续列块（大小[InDim, BN]）。这样对W的访问是连续的。
在该核内部，先做分块的矩阵乘，得到部分和，然后加上对应偏置块的切片，最后逐元素做GELU。

方案B就是MlaProlog这类融合算子的核心思路。 它把原本三个独立的、具有不同数据访问模式的算子，通过精巧的Tiling设计，整合成一个具有连续、规整内存访问模式的超级算子。

下面的流程图展示了从原始子图到最终并行任务映射的设计决策过程：

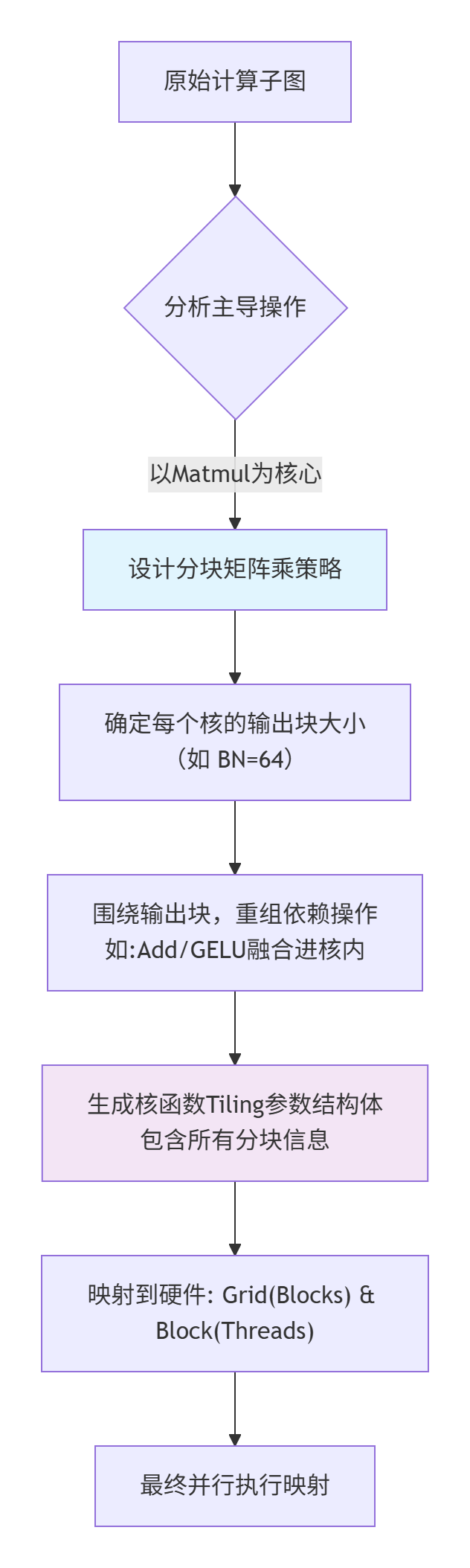
🧩 3.3 第三步：Ascend C Kernel模板选择

别从零开始！CANN生态和社区已经提供了几种成熟的Kernel模板，对应不同的计算模式。选对模板，事半功倍。

向量Element-wise模板：适用于所有输入输出形状完全相同、逐点计算的融合（如Scale+ReLU）。结构最简单，主要是循环展开和向量化加载存储。
分块Matmul核心模板：适用于以矩阵乘为核心，前后缀接Element-wise或广播操作的融合（如Linear+Add+GELU，Attention中的QK^T+Softmax）。这是最复杂也最强大的模板，需要设计Cube（矩阵计算单元）和Vector（向量单元）的协作流水线。MlaProlog就是这个模板的典范。
归约（Reduction）模板：适用于包含Sum、Max等归约操作的融合（如LayerNorm中的均值方差计算）。需要注意同步和树状归约优化。
数据搬运与转换模板：适用于主要功能是数据重排、格式转换（如NHWC转NCHW）的融合。重点优化内存拷贝带宽。

如何选择？ 回到你的计算依赖分析图。找出计算最密集、访存代价最高的那个核心操作。如果它是Matmul，就选用分块Matmul核心模板，并以此为基础，把其他轻量操作“吸附”上去。

🛠️ 3.4 第四步：核内流水线设计与资源分配

选定模板后，就要设计核内部的流水线。目标是让NPU的Cube单元（算矩阵乘）和Vector单元（算激活函数等），以及DMA（数据搬运）都忙起来，互相等待的时间最少。

对于Matmul核心的融合算子，经典的流水线是：

时间步1: DMA将W矩阵的块1从全局内存搬到片上缓存UBuffer A。
时间步2: DMA将X矩阵的块1搬到UBuffer B，同时Cube开始计算W块1 * X块1。
时间步3: DMA搬W块2，Cube计算W块1 * X块2，Vector处理上一轮结果的Add+GELU。
... 如此流水线重叠。

在Ascend C中，这通常通过pipe（流水线）和double_buffer（双缓冲）机制来实现。你需要：

计算每个数据块的大小，确保它能在UBuffer中放下。
安排__pipeline__的producer（生产者，DMA）和consumer（消费者，Cube/Vector）阶段。
为中间结果分配合理的寄存器或UBuffer空间。

一个经验法则：如果融合了复杂的操作，导致核内需要的临时存储（寄存器+UB）超过硬件限制的80%，就应该考虑将融合体拆分成两个更小的、但各自内部依然紧耦合的融合算子。贪多嚼不烂。

📝 3.5 第五步：接口定义与内存规划

最后，设计对外的接口。融合算子通常有多个输入（如X, W, Bias）和输出。

输入：哪些是常量（如训练好的权重W，偏置Bias）？哪些是变量（如输入数据X）？常量可以在算子初始化时就搬到NPU内存并保持不变。
输出：确保输出内存由调用者提前分配好，或者在算子内部分配并返回指针。
Workspace：如果核内需要额外的临时内存（比如用于中间归约），可以通过Workspace机制在运行时申请。在接口中明确Workspace的大小如何计算。

至此，你已经有了一份详细的“建筑图纸”，而不仅仅是模糊的想法。接下来，就是把图纸变成现实的编码阶段。

💻 第四部分实战编码：从蓝图到可运行代码的完整链路

理论说再多，不如一行代码。我们以简化版的 LinearAddGelu融合算子为例，走一遍开发流程。目标：将 Y = X @ W, Z = Y + Bias, Out = GELU(Z)三个操作融合。

📁 4.1 项目结构与脚手架

沿用企业级的标准结构，但为融合算子做一点调整：

fusion_linear_add_gelu/
├── CMakeLists.txt
├── include/
│   ├── common.h
│   ├── kernel_interface.h       // 核函数声明
│   └── tiling_strategy.h        // Tiling参数结构
├── kernel/
│   ├── linear_add_gelu_kernel.cpp   // 核心！！核函数实现
│   └── kernel_utils.cuh         // 一些内核用到的工具函数
├── host/
│   └── linear_add_gelu_host.cpp  // Host侧封装，调用aclrtKernelLaunch
├── test/
│   ├── test_fusion_op.cpp       // 功能与精度测试
│   └── benchmark_fusion_op.cpp  // 性能基准测试
└── scripts/
    ├── build.sh
    └── run_test.sh

⚙️ 4.2 关键代码实现解析

第一步：定义Tiling策略（tiling_strategy.h）

// 决定如何把大矩阵拆成小块
typedef struct {
    // 总体问题规模
    int32_t M; // Batch维度
    int32_t N; // OutDim维度
    int32_t K; // InDim维度
    
    // 每个核（Block）负责的输出块大小
    int32_t BN; // 在N维度（OutDim）上分块，如64
    int32_t BM; // 在M维度（Batch）上分块，如8（适合隐藏维不大的情况）
    
    // 计算总任务网格
    int32_t gridM; // 在Batch维度的块数 = (M + BM - 1) / BM
    int32_t gridN; // 在OutDim维度的块数 = (N + BN - 1) / BN
    
    // 用于GELU的常数（也可在核内硬编码）
    float gelu_const;
} LinearAddGeluTiling;

第二步：核函数实现（kernel/linear_add_gelu_kernel.cpp）- 简化核心逻辑

#include "tiling_strategy.h"

extern "C" __global__ __aicore__ void LinearAddGeluKernel(
    __gm__ float* x,        // 输入 [M, K]
    __gm__ float* w,        // 权重 [K, N]
    __gm__ float* bias,     // 偏置 [N]
    __gm__ float* out,      // 输出 [M, N]
    __gm__ LinearAddGeluTiling* tiling
) {
    // 1. 根据Block ID计算本核负责的输出区域 [m_start:m_end, n_start:n_end]
    int block_id = GET_BLOCK_IDX();
    int grid_n = tiling->gridN;
    
    int n_block = block_id % grid_n;
    int m_block = block_id / grid_n;
    
    int n_start = n_block * tiling->BN;
    int n_len = min(tiling->BN, tiling->N - n_start);
    int m_start = m_block * tiling->BM;
    int m_len = min(tiling->BM, tiling->M - m_start);
    
    if (m_len <= 0 || n_len <= 0) return;
    
    // 2. 在片上内存声明缓存块 (伪代码，实际用__ub__)
    // UBuffer_A: 缓存X的一个小块 [BM, K]
    // UBuffer_B: 缓存W的一个连续列块 [K, BN]
    // UBuffer_C: 累加器，用于存储部分结果 [BM, BN]
    
    // 3. 外层循环：沿着K维度分块加载和计算 (分块矩阵乘)
    for (int k_step = 0; k_step < tiling->K; k_step += BK) { // BK是K维度分块
        int k_len = min(BK, tiling->K - k_step);
        
        // 3.1 DMA异步加载: X的当前块 -> UBuffer_A
        // 3.2 DMA异步加载: W的对应列块 -> UBuffer_B
        
        // 3.3 等待加载完成，并开始计算：Cube单元计算 UBuffer_A * UBuffer_B，累加到 UBuffer_C
        // 这部分是性能核心，会用到__mfma等内置函数或汇编。
    }
    
    // 4. 计算完成后，UBuffer_C中为 [BM, BN] 的中间结果 Y
    // 5. 向量化地加上偏置 Bias 的对应切片 (广播到BM维)
    // 6. 向量化地应用GELU激活函数 (可使用近似公式: x * 0.5 * (1.0 + tanh(sqrt(2/pi) * (x + 0.044715 * x^3))))
    
    // 7. 将最终结果写回全局内存的对应位置
}

关键点注释：

__gm__：指明指针指向全局内存（NPU的HBM），这是核函数参数的标准修饰。
GET_BLOCK_IDX()：获取当前核函数实例的全局索引，是决定“我干哪份活”的关键。
真正的性能代码在第3步：那里需要使用Ascend C的load2d、store2d、mma等内置指令或对CANN基础计算库的调用，来高效实现分块矩阵乘。这里为了可读性做了简化。
向量化：步骤5、6必须使用向量指令，一次处理多个数据。

第三步：Host侧封装（host/linear_add_gelu_host.cpp）

aclError LaunchLinearAddGeluKernel(
    aclrtStream stream,
    const float* x, int M, int K,
    const float* w, int N,
    const float* bias,
    float* out
) {
    // 1. 准备Tiling参数
    LinearAddGeluTiling tiling;
    tiling.M = M; tiling.N = N; tiling.K = K;
    tiling.BM = 8; // 需根据性能测试调整
    tiling.BN = 64; // 需对齐硬件
    tiling.gridM = (M + tiling.BM - 1) / tiling.BM;
    tiling.gridN = (N + tiling.BN - 1) / tiling.BN;
    tiling.gelu_const = 0.044715f;
    
    // 2. 将Tiling参数拷贝到设备端
    void* tiling_dev = nullptr;
    ACL_CHECK(aclrtMalloc(&tiling_dev, sizeof(tiling), ACL_MEM_TYPE_DEVICE));
    ACL_CHECK(aclrtMemcpy(tiling_dev, sizeof(tiling), &tiling, sizeof(tiling),
                         ACL_MEMCPY_HOST_TO_DEVICE));
    
    // 3. 计算启动的核数（总Block数）
    int total_blocks = tiling.gridM * tiling.gridN;
    
    // 4. 调用Runtime API启动核函数
    ACL_CHECK(aclrtKernelLaunch(
        (void*)LinearAddGeluKernel,  // 核函数指针
        total_blocks,               // 启动的Block数
        nullptr,                    // L2配置，高级优化用
        stream,                     // 异步流
        (void*)x, (void*)w, (void*)bias, (void*)out, (void*)tiling_dev // 核函数参数
    ));
    
    // 5. 注意：tiling_dev的内存在stream任务完成后异步释放（需事件同步）
    return ACL_SUCCESS;
}

🔧 4.3 编译、调试与验证闭环

编译脚本（scripts/build.sh）核心：

#!/bin/bash
set -e
BUILD_DIR=build
mkdir -p $BUILD_DIR && cd $BUILD_DIR
# 关键：指定CANN路径下的交叉编译工具链
export ASCEND_CMPP_PATH=/usr/local/Ascend/ascend-toolkit/latest
cmake .. -DCMAKE_C_COMPILER=$ASCEND_CMPP_PATH/bin/aclc \
         -DCMAKE_CXX_COMPILER=$ASCEND_CMPP_PATH/bin/aclc++
make -j8

调试心法：

从CPU仿真开始：先把核函数的逻辑用标准C++写一个CPU版本，验证算法正确性和精度。这是最快的调试方式。
分段验证：在Ascend C内核中，可以先注释掉复杂的流水线和向量化，写一个最简单的、功能正确的“参考实现”版本，确保数据加载和基础计算没错。
使用printf调试（谨慎）：在开发版驱动下，可以有限制地使用printf从核函数内输出少量调试信息，但会极大影响性能且可能刷屏。
依赖Profiler数据：当功能正确后，性能问题全部交给Ascend Insight。看时间线里哪个阶段耗时最长，针对性优化。

验证测试（test/test_fusion_op.cpp）核心：

TEST(FusionLinearAddGelu, Correctness) {
    int M=32, N=256, K=128;
    // 1. 生成随机测试数据 (Host)
    vector<float> h_x(M*K), h_w(K*N), h_bias(N), h_out(M*N), h_ref(M*N);
    generateRandomData(h_x); generateRandomData(h_w); generateRandomData(h_bias);
    
    // 2. 分配Device内存并拷贝数据
    float *d_x, *d_w, *d_bias, *d_out;
    aclrtMalloc(...); aclrtMemcpyH2D(...);
    
    // 3. 运行我们融合的算子
    LaunchLinearAddGeluKernel(stream, d_x, M, K, d_w, N, d_bias, d_out);
    
    // 4. 运行CPU参考实现 (分离的算子组合)
    cpu_reference_linear_add_gelu(h_x.data(), h_w.data(), h_bias.data(), h_ref.data(), M, N, K);
    
    // 5. 拷贝NPU结果回来并对比
    aclrtMemcpyD2H(...);
    float max_diff = computeMaxDiff(h_out, h_ref);
    EXPECT_LT(max_diff, 1e-3f); // 根据数据类型设定误差容忍度
}

🚀 第五部分高阶实战：性能调优与避坑指南

当你的融合算子能跑起来，真正的挑战才开始。下面是我们从MlaProlog等项目里提炼出的“生存手册”。

📈 5.1 性能调优“四步诊断法”

假设你的融合算子性能不如预期，按顺序排查：

第1步：看宏观吞吐与利用率（Ascend Insight摘要页面）

AI Core利用率 < 50%：说明计算密度不够，或者内存带宽是瓶颈。你的融合可能没把计算“压满”。
内存带宽接近峰值但利用率低：访问模式差（如非连续访问），有效带宽低。

第2步：看微观时间线（Trace View）

Kernel内部有大段空白：计算与搬运没重叠好，检查双缓冲和流水线设置。
有大量意想不到的、细小的Memcpy或Cast内核：可能是数据排布不匹配，触发了运行时隐式转换。这是性能的“沉默杀手”，需要调整输入格式或算子内部逻辑来消除。

第3步：看硬件计数器

L1/L2缓存命中率：如果很低，说明数据复用差，考虑调整Tiling大小，让数据块更适应缓存。
向量单元利用率：如果Cube忙但Vector闲，说明Element-wise操作没优化好，或者被内存访问拖累。

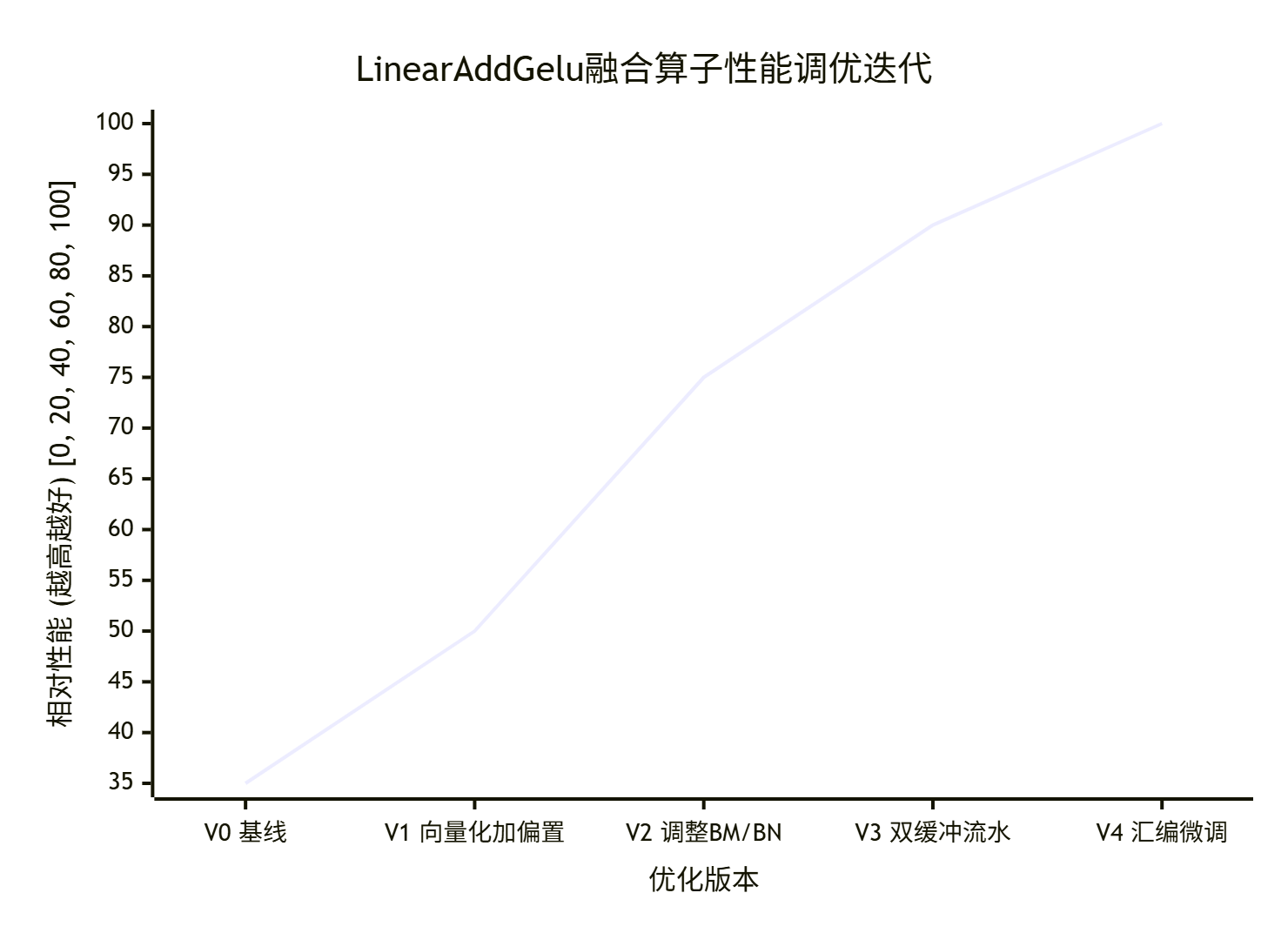
第4步：迭代修改与A/B测试

每次只改一个参数（如BM从8改为16）。
记录修改前后的性能数据（耗时、利用率、带宽）。
如果性能下降，迅速回退，并分析原因。

下面这个真实优化案例的迭代图，展示了如何通过数据驱动优化：

⚠️ 5.2 常见“天坑”与解决方案

数值精度对不上，尤其FP16。
- 现象：与CPU参考结果误差超阈值，特别是在GELU、Softmax等敏感操作后。
- 排查：
  - 检查是否使用了足够的累加精度。例如，FP16的矩阵乘，累加器要用FP32，否则精度损失严重。在Ascend C中，确保mma或相关指令的累加器类型是float。
  - 检查超越函数（如exp, tanh）的近似实现。NPU上可能没有硬件指令，需要用多项式近似。对比不同近似公式在边界值的精度。
  - 解决：采用混合精度策略，关键路径用FP32，非关键用FP16。使用经过验证的数学近似库。
核函数一跑就卡死或复位。
- 现象：aclrtKernelLaunch后设备无响应，或直接报硬件错误。
- 排查（按可能性排序）：
  1. 访问越界：检查所有全局内存访问的索引计算，特别是边界处理（if (idx < total_len)）。
  2. 共享内存/UBuffer超限：检查声明的片上内存大小是否超过硬件限制。
  3. 寄存器溢出导致异常：编译时加-O0暂时关闭优化，看是否还崩溃。如果是，可能需要简化核函数，减少局部变量。
  4. 数据依赖未同步：在核内使用共享内存时，需要__sync_all()确保所有线程写完再读。
- 解决：使用cuda-memcheck类似的工具（CANN可能有acldebug），或者加入大量边界断言和日志，缩小问题范围。
性能随Batch/Size变化诡异，时好时坏。
- 现象：Batch=32时很快，Batch=64时反而慢了。
- 排查：
  - 资源竞争：可能触及了某个硬件资源（如内存通道、缓存bank）的竞争点。用Profiler看不同Batch下的Cache Miss Rate和DRAM Throughput。
  - Tiling策略不适应：你的BM/BN可能对某些尺寸不是最优。考虑实现一个自动调优机制，在算子初始化时，根据问题规模动态选择一组预定义的Tiling参数。
- 解决：实现多套Tiling策略，运行时选择。这是高性能库的常见做法。

🔮 5.3 前瞻：融合算子的未来与你的机会

编译器自动化融合：未来，像CANN图编译器会更加智能，能自动识别可融合的子图模式，并生成优化代码。但自定义融合仍会存在，用于那些最核心、最定制化的计算模式。
领域特定融合库：会出现针对视觉、语音、科学计算等领域的专用融合算子库，就像cuDNN、oneDNN一样。提前深入某个领域，建立自己的算子壁垒，是很大的机会。
软硬协同设计：下一代NPU架构可能会为特定的融合模式（如Attention）设计更高效的硬件单元。理解算法和硬件的协同，会让你站在创新的前沿。