DartQuant:基于分布转换的旋转量化算法
由于INT4表达能力有限,以及大模型激活异常值分布显著,大模型W4A4 INT4量化面临严峻的精度损失风险。本文分析了旋转量化的数学原理,并提出了基于分布转换的旋转量化算法(DartQuant),通过激活数据分布的平坦化,可有效降低W4A4量化误差。
摘要
由于INT4表达能力有限,以及大模型激活异常值分布显著,大模型W4A4 INT4量化面临严峻的精度损失风险。本文分析了旋转量化的数学原理,并提出了基于分布转换的旋转量化算法(DartQuant),通过激活数据分布的平坦化,可有效降低W4A4量化误差。
一、背景
昇腾A2/A3硬件支持INT4/INT8格式,W4A4比W8A8能够进一步压缩模型、提升推理性能。然而,W4A4量化面临严峻的精度损失挑战,特别是在高精度任务中(如Reasoning、Function call),精度损失不可忽视。我们提出了基于分布转换的旋转量化方法,通过精确优化旋转矩阵,能够有效缓解W4A4量化的精度误差,提升量化后模型的精度。这一方法不仅适用于昇腾NPU,也能广泛应用于各种低精度计算平台,为实际生产环境中的模型部署提供了更加高效、精确的解决方案。
二、异常值抑制:从SmoothQuant到旋转量化
众所周知,大模型权重激活量化面临的首要问题便是激活异常值(outliers)的影响,异常值被饱和截断(增加截断误差)或包含在量化动态范围(增加舍入误差),都会引起较大的量化误差。通过per-channel scaling与bias correction,可有效降低跨通道数据分布差异、并提升数据分布的对称性,是W8A8量化抑制异常值影响的常用方法:
| 算法 | 简要说明 |
| SmoothQuant | per-channel scaling,降低跨通道数据分布差异 |
| Outlier suppression+ | per-channel scaling与bias correction,且优化搜索smooth scale,降低跨通道数据分布差异、并提升数据分布的对称性 |
| OmniQuant | 针对每个sub-module,引入可训练SmoothQuant |
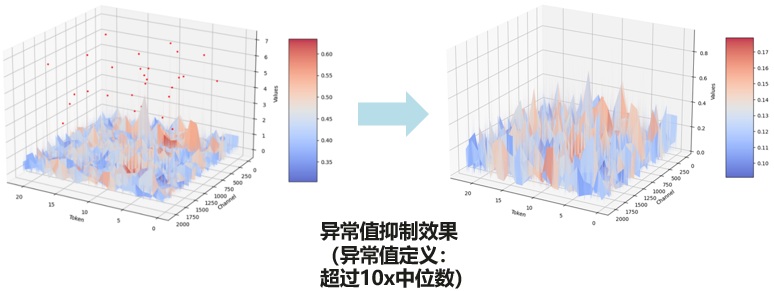
昇腾A2/A3 NPU、以及NV A100 GPU等硬件支持INT4数值格式,为进一步提升大模型推理性能,W4A4 INT4量化进入大众视野。W4A8量化仍可通过两级量化、per-channel scaling等策略保证精度(参考Qserve),然而W4A4量化面临如下技术挑战:
- 平坦度:INT4量化步长是均匀的,适合高斯分布(偏集中分布)或均匀分布;
- 偏斜度:数据分布呈现非对称或偏斜时,W4A4需采用非对称量化,但表达能力有限;
- 异常值分布:INT4动态范围窄,若数据分布偏离均匀分布、outlier占比较高,引起W4A4量化误差。
旋转矩阵变换是降低激活异常值分布水平的有效方法,旋转变换之后激活数据的主分布基本不变(如均匀分布或高斯分布)、而outlier分布水平显著降低,因此可使数据分布平坦化(或近高斯分布),有助于大幅降低W4A4量化误差:
|
算法 |
简要说明 |
|
QuIP |
Weight-only旋转变换 |
|
QuaRot |
正交Hadamard旋转变换,同时应用于权重与激活 |
|
DuQuant |
通过旋转与重排,降低异常值分布水平 |
|
SpinQuant |
引入可训练旋转变换,由于全局共享R1矩阵,端到端训练开销大 |
|
OSTQuant |
联合可训练旋转变换与per-channel scaling,端到端训练开销大 |
|
FlatQuant |
联合可训练仿射变换与per-channel scaling;不同layer采用不同的仿射变换矩阵,layer-wise训练可降低离线开销,但无法被等价吸收,依赖Kronecker分解降低在线矩阵乘开销 |
|
DartQuant |
可训练正交旋转变换,离线训练校准开销低,且旋转矩阵可被等价吸收 |
如上表所示,旋转量化从早期的Hadamard变换(QuaRot)、演进到可训练方式(如SpinQuant、FlatQuant)。然而,类似SpinQuant,基于离线训练的量化校准存在较高的应用成本;另一方面,类似FlatQuant,在线变换矩阵不能被等价吸收,导致在线计算开销上升,影响模型的端到端推理性能。针对上述两个问题,本文提出了基于可训练正交旋转变换的DartQuant量化算法,在保证低离线校准成本的同时,能确保旋转矩阵被等价吸收,从而提供了高效、且精确的W4A4量化方案。DartQuant旋转矩阵设置与SpinQuant相同,如下图所示:
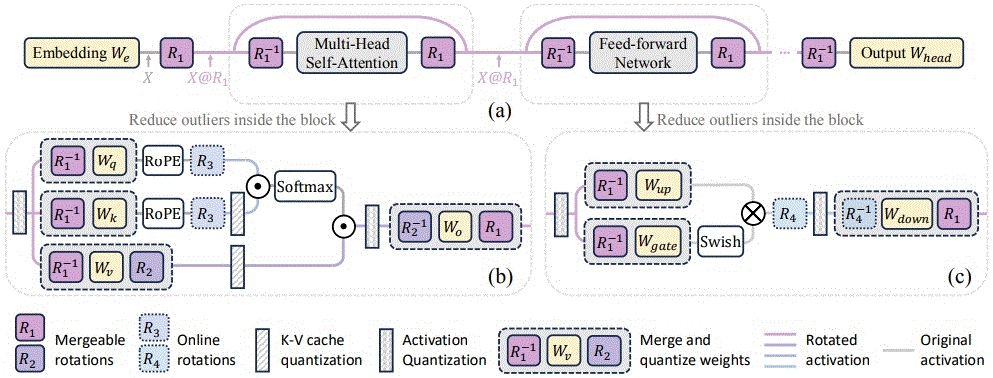
三、DartQuant算法原理
基于分布变换的旋转矩阵量化算法 (DartQuant) 如下图所示,基于激活正交旋转变换降低异常值水平,且通过低成本的离线训练校准方法获得正交变换矩阵:
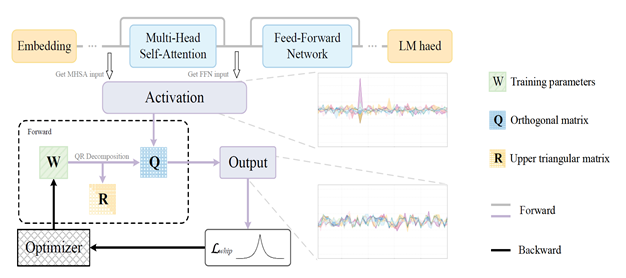
DartQuant正交旋转量化的具体原理如下:
- 旋转矩阵分离校准框架:实现旋转量化校准与LLM推理的解耦,大幅降低校准显存需求,加快校准速度;
- 高效的Whip损失:基于Whip loss约束旋转后激活,使其趋向均匀分布,亲和INT4均匀量化,降低量化误差。并且Whip损失计算简单,连续可导,比MSE量化误差等优化目标更容易优化;
- 高效的正交优化:通过结合QR分解与常规优化器设计了一种正交约束优化方案,降低了正交优化的计算复杂度,加快了旋转矩阵校准速度;
- 正交旋转量化:基于正交矩阵R,对线性层输入激活进行旋转量化;R的作用位置包括R1、R2矩阵等。
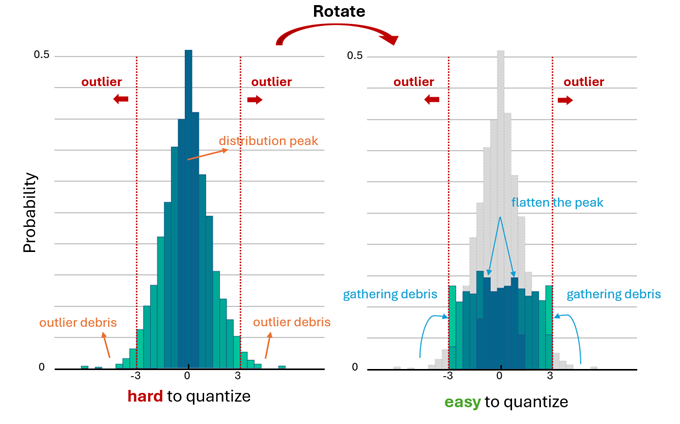
激活分布通常接近拉普拉斯分布,数据大部分集中在均值 0 附近,仅有少量较大的离群值位于远离数据中心的区域。理想的激活分布转换:原本中心区域数值扩展到了更广泛的区间,从而平滑了分布尖峰。与此同时,远离中心的离群点聚集到一起,缩小了分布范围,最终在区间[−3, 3]内形成了近似均匀分布。
受分布转换机制启发,本文提出了分布转换调整函数(Whip函数),该函数在接近零值的区域具有较大的梯度,当将其用作优化目标时,旋转后的激活向量中的小值会被 “推离” 零值。在模不变的约束下,离群值(outliers)被 “聚集” ,从而促使旋转后的激活趋向一个更小范围内的均匀分布趋向均匀分布的激活与均匀量化更加契合,从而有效降低量化误差。此外,分布转换调整函数函数具有连续可导性,相较于直接使用量化损失作为优化目标,它更容易进行优化。
四、实验效果
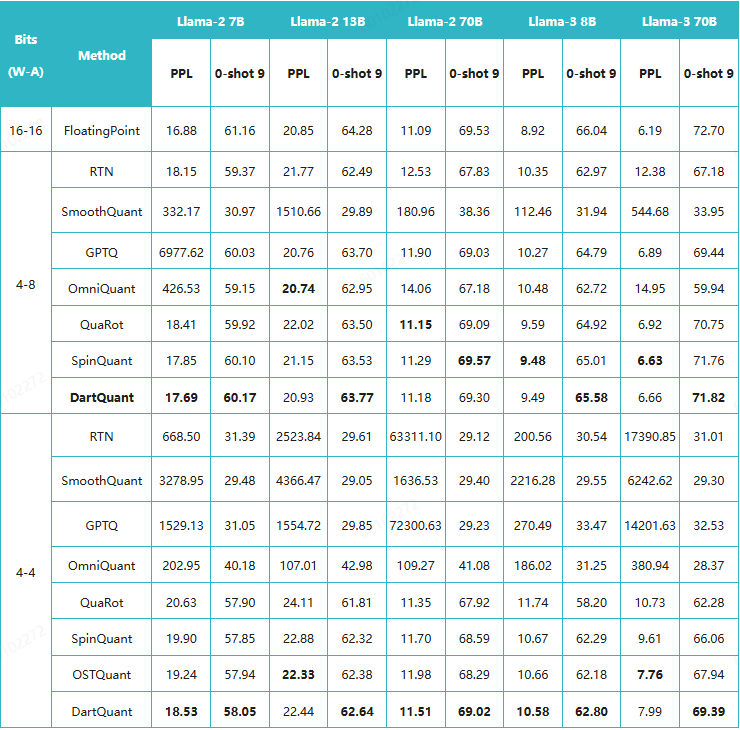
针对W4A4 INT4,通过DartQunt达成如下实验效果:
- Llama2-70B W4A8通用任务精度损失<0.5%;
- Llama2-70B+W4A4/A8混精精度损失<1.5%;
- 额外在Llama2-7B、Llama2-13B、Llama-3 70B、Mixtral-7×8B等模型上增加W4A8、W4A4等的摸高测试,增加5+测试集,优于Quarot、SpinQuant、OSTQuant等业界SOTA算法,证明了量化算法的泛化性;
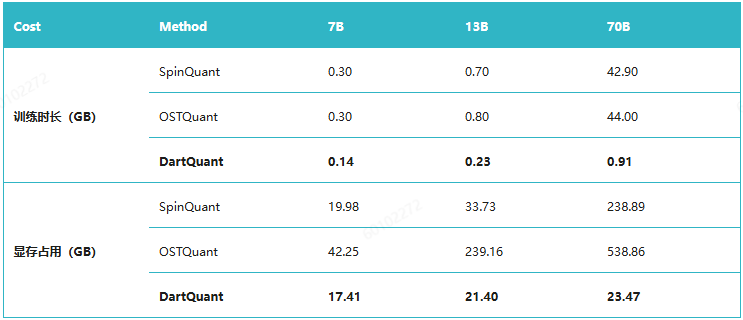
- 大幅降低离线训练校准的成本,单卡小时级完成旋转矩阵校准(Llama2-7B 单卡45分钟完成校准),并且显存成本降低2x~20x。
DartQuant与其他业界SOTA算法的量化精度对比如下:
DartQuant离线校准成本如下:

鲲鹏昇腾开发者社区是面向全社会开放的“联接全球计算开发者,聚合华为+生态”的社区,内容涵盖鲲鹏、昇腾资源,帮助开发者快速获取所需的知识、经验、软件、工具、算力,支撑开发者易学、好用、成功,成为核心开发者。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容







所有评论(0)