作者：昇腾实战派

 

1、背景概述

在深度学习中，算子的确定性计算对于确保模型训练和推理的可复现性至关重要。然而，许多算子（如均值计算算子）在默认实现下可能存在非确定性问题，尤其是在float32数据类型上，这是由于浮点数计算不满足结合律，导致多核并行计算顺序不一致引入的数值偏差。本文以mean算子为例，系统性地复现了其在GPU和NPU上的非确定性计算问题，对比了确定性实现与非确定性实现的性能差异，并探索了通过Triton框架在NPU上的适配与优化策略。实验表明，确定性实现能消除结果波动，但会带来显著的性能开销，为实际应用中的需要进行权衡。

repo仓库链接：https://github.com/thinking-machines-lab/batch_invariant_ops

 

2、确定性问题复现

首先依据官方给出的操作步骤复现该算子的确定性计算问题。

a) 安装batch_invariant_ops库

git clone https://github.com/thinking-machines-lab/batch_invariant_ops
pip install -e .

b) 改写测试脚本

原仓中的测试用例test_batch_invariance.py，提供了matmul算子的确定性结果演示；为复现mean算子的问题，需要进行一些改写，代码如下：

import torch
from batch_invariant_ops import set_batch_invariant_mode

device_type = getattr(torch.accelerator.current_accelerator(), "type", "cpu")
print(device_type)
torch.set_default_device(device_type)

# Just to get the logging out of the way haha
with set_batch_invariant_mode(True):
    pass

def test_batch_invariance(dtype=torch.float32):
    B, D, X = 2048, 4096, 16
    a = torch.linspace(-100, 100, B*D*X, dtype=dtype).reshape(B, D, X)

    # Method 1: vector multiplication (batch size 1)
    out1 = torch.mean(a[:1], dim=1, keepdim=False)

    # Method 2: Matrix multiplication, then slice (full batch)
    out2 = torch.mean(a, dim=1, keepdim=False)[:1]

    # Check if results are identical
    diff = (out1 - out2).abs().max()

    return diff.item() == 0, diff

def run_iters(iters=10):
    for dtype in [ torch.float32 , torch.bfloat16 ]:
        is_deterministic = True
        difflist = []
        for i in range (iters):
            isd, df = test_batch_invariance(dtype)
            is_deterministic = is_deterministic and isd
            difflist.append(df)
        print( f"Batch Deterministic: {is_deterministic} run-to-run max/min/diff {max(difflist)}/{min(difflist)}/{max(difflist)-min(difflist)} for {dtype} in {iters} iterations")


# Test with standard PyTorch (likely to show differences)
# shows that: in standard mode, the results may have some diffs
print("Standard PyTorch:")
with set_batch_invariant_mode(False):
    run_iters()
  
# Test with batch-invariant operations
print("\nBatch-Invariant Mode:")
with set_batch_invariant_mode(True):
    run_iters()
# shows that: in batch_invariant mode，the results are all the same

该示例设置输入尺寸为（2048，4096, 16）；为全面评测算子性能，需要覆盖更多输入场景。运行结果如下：

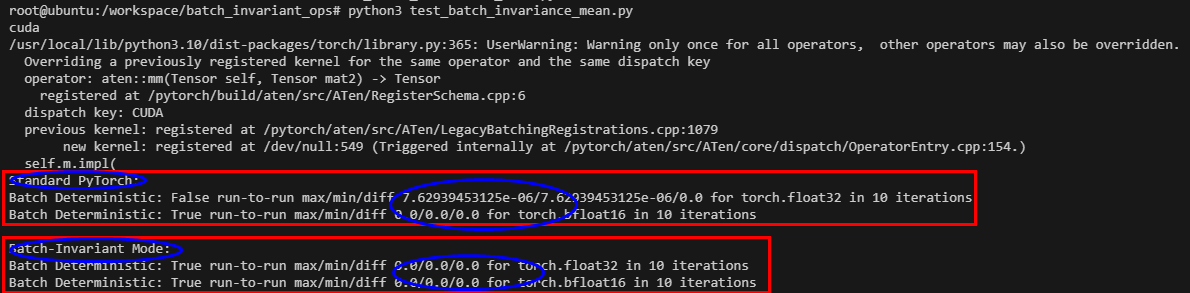
可以看到，在pytorch标准模式下，对于float32数据格式出现了不确定性计算的问题；而在batch-invariant mode下，float32数据格式下计算结果是确定的。

——值得一提的是：在bfloat16数据格式下，两种模式下的计算结果都是确定的。

c) 性能差异比较

一般来说，为了实现确定性计算，需要牺牲一些性能。那么，对于该算子确定性实现和非确定性实现之间的性能差异有多大呢？

import torch

import triton
import triton.language as tl

@triton.jit
def mean_kernel(
    input_ptr,
    output_ptr,
    input_stride0,
    input_stride1,
    input_stride2,
    output_stride0,
    output_stride1,
    M,  # size before reduction dim
    N,  # size of reduction dim
    K,  # size after reduction dim
    BLOCK_SIZE: tl.constexpr,
):
    """
    Kernel for computing mean along a single dimension.
    Input is viewed as (M, N, K) where N is the dimension being reduced.
    """
    # Program ID gives us which output element we're computing
    pid = tl.program_id(0)

    # Compute output indices
    m_idx = pid // K
    k_idx = pid % K

    # Bounds check
    if m_idx >= M or k_idx >= K:
        return

    # Accumulate sum across reduction dimension
    acc = 0.0
    for n_start in range(0, N, BLOCK_SIZE):
        n_offsets = n_start + tl.arange(0, BLOCK_SIZE)
        mask = n_offsets < N

        # Calculate input indices
        input_idx = m_idx * input_stride0 + n_offsets * input_stride1 + k_idx * input_stride2

        # Load and accumulate
        vals = tl.load(input_ptr + input_idx, mask=mask, other=0.0)
        acc += tl.sum(vals)

    # Compute mean and store
    mean_val = acc / N
    output_idx = m_idx * output_stride0 + k_idx * output_stride1
    tl.store(output_ptr + output_idx, mean_val)

def mean_dim(
    input: torch.Tensor, dim: int, keepdim: bool = False, dtype: torch.dtype | None = None
) -> torch.Tensor:
    """
    Triton implementation of torch.mean with single dimension reduction.

    Args:
        input: Input tensor
        dim: Single dimension along which to compute mean
        keepdim: Whether to keep the reduced dimension
        dtype: Output dtype. If None, uses input dtype (or float32 for integer inputs)

    Returns:
        Tensor with mean values along specified dimension
    """
    # Validate inputs
    assert input.is_cuda, "Input must be a CUDA tensor"
    assert -input.ndim <= dim < input.ndim, (
        f"Invalid dimension {dim} for tensor with {input.ndim} dimensions"
    )

    # Handle negative dim
    if dim < 0:
        dim = dim + input.ndim

    # Handle dtype
    if dtype is None:
        if input.dtype in [torch.int8, torch.int16, torch.int32, torch.int64]:
            dtype = torch.float32
        else:
            dtype = input.dtype

    # Convert input to appropriate dtype if needed
    if input.dtype != dtype:
        input = input.to(dtype)

    # Get input shape and strides
    shape = list(input.shape)

    # Calculate dimensions for kernel
    M = 1
    for i in range(dim):
        M *= shape[i]

    N = shape[dim]

    K = 1
    for i in range(dim + 1, len(shape)):
        K *= shape[i]

    # Reshape input to 3D view (M, N, K)
    input_3d = input.reshape(M, N, K)

    # Create output shape
    if keepdim:
        output_shape = shape.copy()
        output_shape[dim] = 1
    else:
        output_shape = shape[:dim] + shape[dim + 1 :]

    # Create output tensor
    output = torch.empty(output_shape, dtype=dtype, device=input.device)

    # Reshape output for kernel
    if keepdim:
        output_2d = output.reshape(M, 1, K).squeeze(1)
    else:
        output_2d = output.reshape(M, K)

    # Launch kernel: in npu: you must limit that the max_grids is 48
    grid = (M * K,)   
    BLOCK_SIZE = 1024

    mean_kernel[grid](
        input_3d,
        output_2d,
        input_3d.stride(0),
        input_3d.stride(1),
        input_3d.stride(2),
        output_2d.stride(0),
        output_2d.stride(1) if output_2d.ndim > 1 else 0,
        M,
        N,
        K,
        BLOCK_SIZE,
    )

    return output

if __name__=="__main__":
    import torch
    import time
    torch.rand(42)

    device_type = getattr(torch.accelerator.current_accelerator(), "type", "cpu")
    print(device_type)
    torch.set_default_device(device_type)
    repreat_num = 100
    warmup_time = 3

    #1. construct input
    B, D, X = 2048, 4096, 16
    input = torch.linspace(-100, 100, B*D*X, dtype = torch.float32).reshape(B, D, X)

    #2. run, get profiling data
    for i in range(warmup_time):
        output = mean_dim(input, dim=1, keepdim=False)
  
    start = time.time()
    for i in range(repreat_num):
        output = mean_dim(input, dim=1, keepdim=False)
    torch.cuda.synchronize()
    end = time.time()
    print("the time elapsed for shape {}, {} is {}ms".format(B, D, (end - start) * 1000 / repreat_num))

    #3. compare with torch implementation
    for i in range(warmup_time):
        output = torch.mean(input, dim=1, keepdim=False)
  
    start = time.time()
    for i in range(repreat_num):
        output = torch.mean(input, dim=1, keepdim=False)
    torch.cuda.synchronize()
    end = time.time()
    print("for torch implementation, the time elapsed for shape {}, {} is {}ms".format(B, D, (end - start) * 1000 / repreat_num))

可以看到，对于（2048,4096,16）这种输入shape来说，mean确定性计算的实现耗时会大大增加，性能约为非确定性实现的1/3。GPU卡型号为96G H20

d) NPU下问题是否存在

在NPU下，是否存在类似问题， 即Ascend-C算子是否实现了确定性计算呢？ 实验如下：

import torch
from batch_invariant_ops import set_batch_invariant_mode

device_type = getattr(torch.accelerator.current_accelerator(), "type", "cpu")
print(device_type)
torch.set_default_device(device_type)

def test_batch_invariance(dtype=torch.float32):
    B, D, X = 2048, 4096, 16
    a = torch.linspace(-100, 100, B*D*X, dtype=dtype).reshape(B, D, X)

    # Method 1: Matrix-vector multiplication (batch size 1)
    out1 = torch.mean(a[:1], dim=1, keepdim=False)

    # Method 2: Matrix-matrix multiplication, then slice (full batch)
    out2 = torch.mean(a, dim=1, keepdim=False)[:1]

    # Check if results are identical
    diff = (out1 - out2).abs().max()

    return diff.item() == 0, diff

def run_iters(iters=10):
    for dtype in [ torch.float32 , torch.bfloat16 ]:
        is_deterministic = True
        difflist = []
        for i in range (iters):
            isd, df = test_batch_invariance(dtype)
            is_deterministic = is_deterministic and isd
            difflist.append(df)
        print( f"Batch Deterministic: {is_deterministic} run-to-run max/min/diff {max(difflist)}/{min(difflist)}/{max(difflist)-min(difflist)} for {dtype} in {iters} iterations")


# Test with standard PyTorch (likely to show differences)
# shows that: in standard mode, the results may have some diffs
print("Standard PyTorch:")
with set_batch_invariant_mode(False):
    run_iters()

可以看到，在NPU上，非确定性计算的问题也会存在，且只会出现在float32数据类型上。

2、NPU适配

该repo下的算子均为triton实现，因此在NPU下的适配可以走triton-ascend适配路径。当然，也可以用Ascend-C去实现一版确定性的mean计算，该实现方式不在本文讨论范围内。

a) 安装triton-ascend

目前官方提供daily包，采用daily包安装方式，找到对应的安装命令：

pip install -i https://test.pypi.org/simple/ triton-ascend==3.2.0.dev2025112001

daily包查询路径：https://test.pypi.org/project/triton-ascend/3.2.0.dev2025112001/#history

b) 适配跑通

安装triton-ascend之后，后续的triton操作默认都是执行在npu上；无需额外import triton-ascend。

triton-ascend期望达到的适配效果是仅需修改少量代码，即可完成算子的NPU适配，对于上面的代码，需要做如下几处适配修改，如下图所示：

• 导入torch_npu

• torch.cuda -> torch.npu

运行测试脚本，结果如下：

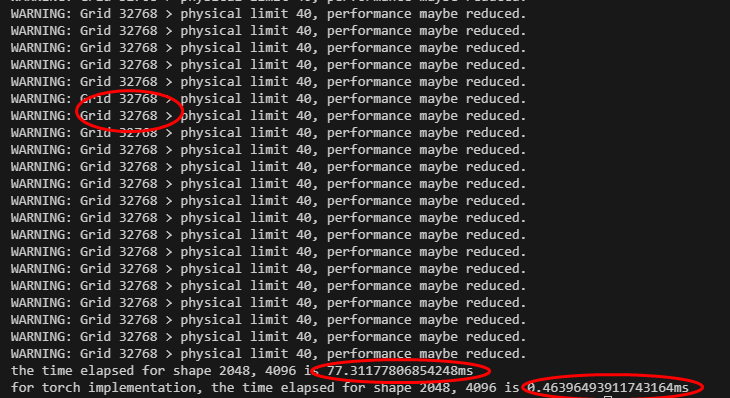
可以看到算子可以正常运行，不过提示Grid数过多，物理限制为40个，可能导致性能下降。 实际的耗时结果如下：

triton实现（确定）	Ascend-C实现（非确定）	耗时比例
77.31ms	0.46ms	168x

c) 性能优化

确定性计算的实现思想是把规约操作尽量放在单核上进行，避免多核执行顺序不一致以及float数据类型不满足结合律特性引入不确定性。结合WARN提示，和代码实现逻辑来看，Grid设置太大，超过了物理核的实际个数，会

引入较大的开销。 因此结合该算子的实现，可以设计如下几种优化思路：

• 每个Grid对应M轴；
• 每个Grid对应K轴；
• 若M轴很大，则Grid设为40，每个Grid处理M轴多行；
• 若K轴很大，则Grid设为40，每个Grid处理K轴多列；
• 输入进行reshape，变换为(M,K,N);  使要处理的数据位于尾轴；
• 对Block_Size进行优选

详细实验结果如下所示：

序号	triton确定性	Ascend-C非确定性	Grid数	耗时比	分析
每个Grid对应M轴	45.69	0.467	2048	97.83X	逻辑Grid数 》物理核数，引入较大开销；存在进一步优化空间；相较于之前的32768，grid数已大大减少
每个Grid对应K轴	226.12	0.468	16	484.20X	1. 物理核数未打满；2. K轴数据存储不连续，数据读取耗时会比较大
Grid设为40，每个Grid处理M轴离散多行	46.17	0.468	40	98.65X	逻辑核降到40，略有上升，why?
Grid设为40，每个Grid处理M轴连续多行	46.07	0.468	40	98.44X	逻辑核降到40，略有上升，why?
输入reshape为(M,K,N);	2.75	0.468	2048	5.87X	数据处理发生在尾轴，因数据连续，读写开销会大幅减少
对Block_Size进行优选（512-》8192）	1.78	0.468	2048	3.8X	尽量增大UB使用大小，减小循环次数
2048 thread -> 40 thread	1.80	0.468	40	3.84X	将逻辑核降低到40，略有上升
合并为M * K,  均分到40thread处理	1.83	0.468	40	3.91X	引入比较多的标量计算

 

3、总结

• GPU和NPU，Pytorch官方API,  mean算子在float32数据类型下均存在不确定性计算问题，float16无该问题；
• NPU下也存在不确定性问题；
• GPU下采用triton实现的mean确定性计算算子，会导致算子性能下降为CUDA实现的1/3;
• 采用triton-ascend适配mean算子，算子性能下降幅度与GPU类似。

 

4、参考资料

https://lmsys.org/blog/2025-09-22-sglang-deterministic/

https://thinkingmachines.ai/blog/defeating-nondeterminism-in-llm-inference/

https://zhuanlan.zhihu.com/p/1956415532606665583

https://gitcode.com/Ascend/triton-ascend/blob/master/docs/HighPerformanceGuide.md