一、为什么要在训练中使能GMM NZ？

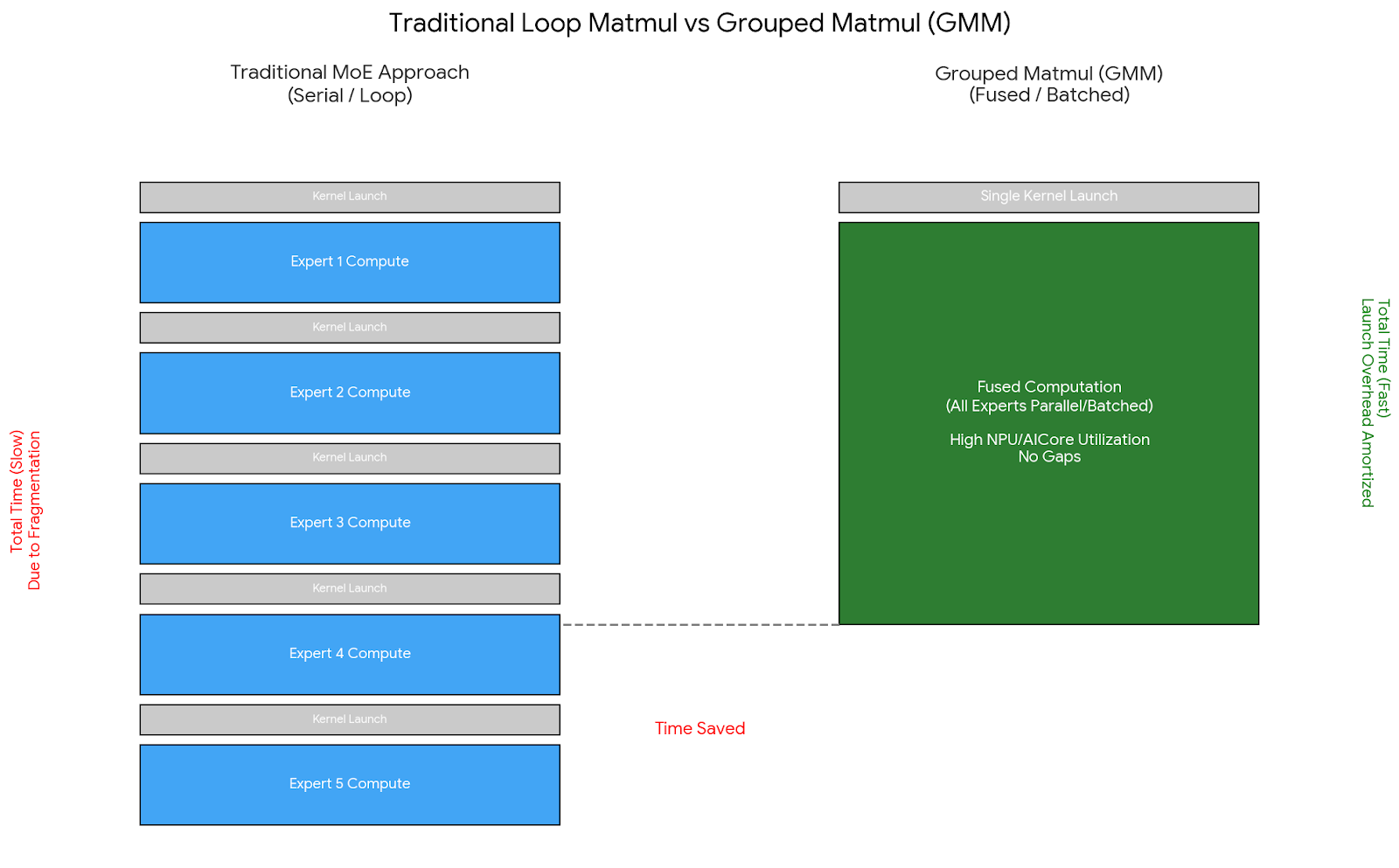
训练 Qwen3 235B 这种量级的 MoE 模型，最大的拦路虎往往不是显存墙，而是计算碎片化。MOE 架构虽然通过动态路由扩展了容量，但这种机制天然引入了海量的小矩阵乘法。如果直接使用传统的 Matmul 算子，大量的时间会被浪费在内核启动（Kernel Launch）和内存搬运上，AICore 的利用率极低。

这正是 Grouped Matmul (GMM) 登场的理由。不同于 NVIDIA GPU 上借鉴 cuBLAS batch Matmul 的思路，Ascend NPU 的 GMM 算子不仅要解决多专家并行计算的问题，还要深度适配华为特有的 NZ (Fractal) 内存格式，以压榨出极致的访存性能。但在训练场景（涉及反向传播与 FSDP 通信）中强行“使能”这一特性，远比推理要复杂得多。

当然，MOE训练的痛点不止计算碎片。专家路由导致token分配不均，传统Matmul逐专家计算会放大开销。GMM通过分组融合，利用NPU的并行单元（如AICore）高效处理。根据实践，在多卡环境中，使能GMM NZ可缩短单步时间10%-20%，但需小心格式转换的隐形成本。这在其他硬件如NVIDIA GPU上，也可借鉴cuBLAS的batch Matmul，但Ascend的aclnn接口更注重稀疏兼容。

---

二、PTA中GMM算子的深度适配与优化

以torch_npu.npu_grouped_matmul为例，本文详解了GMM的批量矩阵乘融合机制，能合并相似形状操作，降低内存访问和计算负载。

2.1 算子核心原型剖析

在非量化、无偏置条件下，计算公式为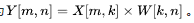
。关键参数包括：

• group_list (tokens_per_expert)：沿X的m轴（batch/token维度）切分，每个专家获配token数，体现MOE路由动态性。
• group_type：-1不分组；0切m轴（token分配常见）；1切weight n轴；2切k轴（反向计算用）。
• group_list_type：1为组元素个数；2为起止索引。
• split_item：0/1输出多张量（与weight数匹配）；2/3输出单张量（便于concat）。

示例：X.shape = [m, k]，weight.shape = [num_expert, k, n // num_expert]，代码：

outs = torch_npu.npu_grouped_matmul([x], [weight], group_list=tokens_per_expert, group_type=0, group_list_type=1, split_item=2)[0]

这将X按m轴分num_expert份，每份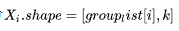
，对应weight第i专家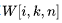
。输出单张量[m, n]。

GMM 的核心价值在于“拒绝空转”。传统的逐专家 Matmul 相当于让 NPU 频繁地“启动-刹车”，尤其当专家数达到 128+ 时，Kernel Launch 的开销甚至可能超过计算本身。GMM 通过单次 Kernel 发射处理所有专家的计算，配合 group_type=0 模式，还能自动处理 MoE 路由产生的 Token 负载不均问题，确保 NPU 的矢量计算单元时刻处于饱和状态。

2.2 前向与反向传播的自定义实现

原算子不支持反向，需手动推导梯度：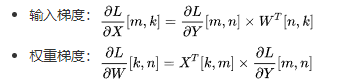

反向用GMM实现：

# 输入梯度
grad_input = torch_npu.npu_grouped_matmul([grad_output], [weight.transpose(1,2)], group_list=tokens_per_expert, group_type=0, group_list_type=1, split_item=2)[0]
# 权重梯度
grad_weight = torch_npu.npu_grouped_matmul([input_tensor.T], [grad_output], bias=None, group_list=tokens_per_expert, split_item=3, group_type=2, group_list_type=1)[0]

权重梯度时，对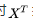
按k轴切，故group_type=2。

完整autograd Function：

from torch.autograd import Function
import torch_npu
from torch_npu import transfer_to_npu

class NpuGMMOp(Function):
    @staticmethod
    def forward(ctx, weight, x, tokens_per_expert):
        ctx.save_for_backward(weight, x, tokens_per_expert)
        outs = torch_npu.npu_grouped_matmul([x], [weight], group_list=tokens_per_expert, group_type=0, group_list_type=1, split_item=2)[0]
        return outs

    @staticmethod
    def backward(ctx, grad_output):
        weight, input_tensor, tokens_per_expert = ctx.saved_tensors
        grad_input = torch_npu.npu_grouped_matmul([grad_output], [weight.transpose(1,2)], group_list=tokens_per_expert, group_type=0, group_list_type=1, split_item=2)[0] 
        grad_weight = torch_npu.npu_grouped_matmul([input_tensor.T], [grad_output], bias=None, group_list=tokens_per_expert, split_item=3, group_type=2, group_list_type=1)[0]
        return grad_weight, grad_input, None

if __name__ == "__main__":
    out = NpuGMMOp.apply(weight, x, tokens_per_expert)

PyTorch autograd依赖Function定义自定义op。ctx保存前向变量避重算。反向transpose是瓶颈，后文详解消除。在CUDA中，可用torch.autograd.function类似，但Ascend aclnn更注重NZ兼容。实践时，需测试梯度精度，避免bfloat16溢出。

---

三、训练场景下GMM NZ的技术方案探索

3.1 手动转NZ示例

推理中，权重转NZ后GMM直接输出ND，性能优。但训练权重更新频繁，简单迁移失效。

手动转NZ尝试：

weight = weight + 0
weight = torch_npu.npu_format_cast(weight, 29)
out = NpuGMMOp.apply(weight, x, tokens_per_expert)

结果：transdata开销抵消收益。训练中转格式O(n)耗时累积。

NZ（FRACTAL_NZ）是Ascend分块稀疏，16x16块只存非零，减访存50%+。但训练梯度破坏稀疏，动态转NZ昂贵。在GPU上，类似cuSPARSE，但训练稀疏更新复杂。需融合操作规避。

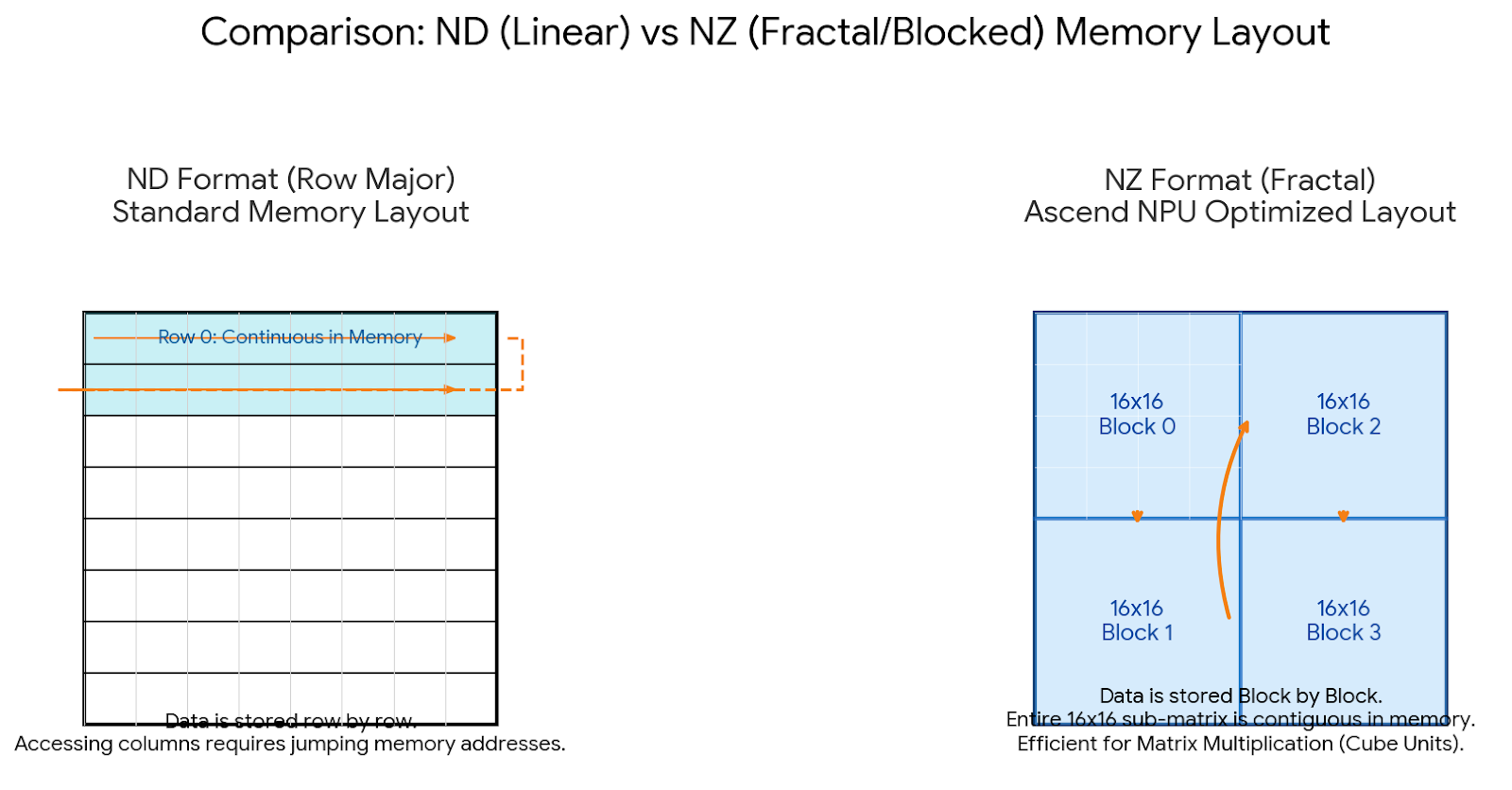
3.2 sliceNZ算子的设计与必要性

FSDP2权重流程：初始化分片 → 加载 → AllGather → slice → GMM。slice（torch.split_with_sizes_copy）和转NZ均HBM搬运，可融合。slice前置，不干扰他op。

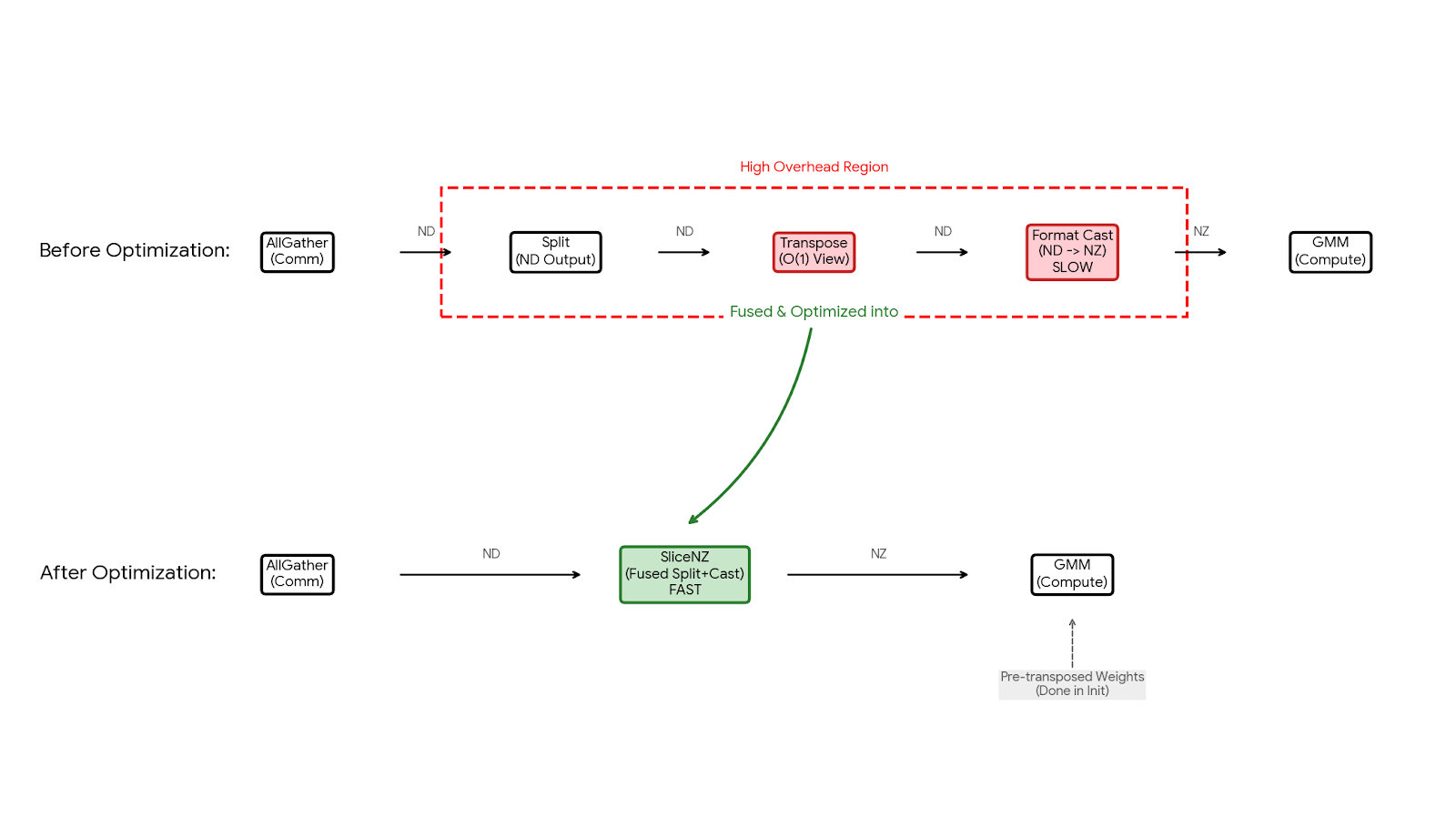
原slice：

@torch.library.impl(lib, "split_with_sizes_copy", "PrivateUse1")
def split_with_sizes_copy(all_gather_output, all_gather_input_split_sizes, dim, out):
    torch.split_with_sizes_copy(all_gather_output, all_gather_input_split_sizes, dim=dim, out=out)

sliceNZ原型：aclnn接口，切并转NZ。

aclnnSliceNzGetWorkspaceSize(const aclTensor *in, uint64_t dim, uint64_t start, uint64_t end, aclTensor *output)

output 3D [num_expert, n, k] 或2D。

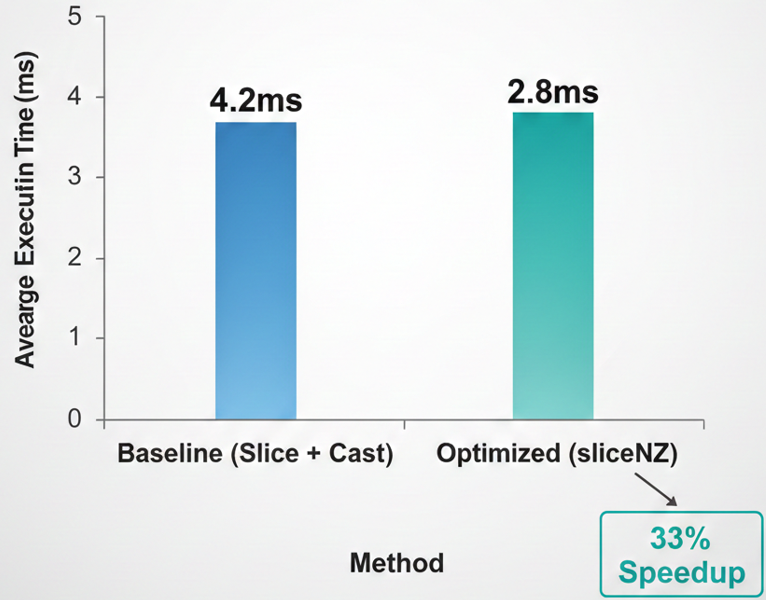
为了验证 sliceNZ 融合算子的实际收益，我们在单节点 8xNPU 环境下，针对 Qwen3-235B 的一个 MoE 层进行了 Micro-benchmark 测试。对比了“原生 Slice + 格式转换”与“融合 sliceNZ”的耗时情况。如下图所示，在专家并行度为 128 的配置下，sliceNZ 将原本碎片化的搬运和转换操作合并，单层算子执行耗时从 4.2ms 降低至 2.8ms，端到端性能提升显著。

---

四、PTA框架中sliceNZ的集成使能

4.1 适配结构化过程

op_plugin_functions.yaml添加：

- func: npu_special_slice(Tensor self, int dim, int start, int end, Tensor(a!) output) -> ()
  op_api: [v2.1, newest]
  gen_opapi:
    exec: aclnnSliceNz, self, dim, start, end, output

无反向，无改derivatives。避关键字冲突。

4.2 PTA包编译与部署

用v2.6.0分支（含k轴切）。docker编包避污染。命令如图（描述：dockerfile和编译输出截图）。

安装新PTA+CANN后，torch_npu.npu_special_slice可用。

FSDP2 patch：识GMM weight内存，view 3D，调sliceNZ，他op原slice。

@torch.library.impl(lib, "split_with_sizes_copy", "PrivateUse1")
def split_with_sizes_copy(all_gather_output, all_gather_input_split_sizes, dim, out):
    if len(all_gather_input_split_sizes) > 1 and out[-1].shape[0] * out[-1].shape[1] >= 128 * 4096*1536:
        from special_op import npu_special_slice
        # ... (计算start/end，resize out[-1/-2]为3D)
        npu_special_slice(all_gather_output, dim, weight_1_start, total_size, out[-1])
        npu_special_slice(all_gather_output, dim, weight_2_start, weight_1_start, out[-2])
        # ... (其他tensor用原split)
        return

猴子补丁无缝集成。在多卡，结合NCCL优通信。编包坑：版本Mismatch致接口缺，用A3测。

---

五、PTA格式校验机制的绕过

使能后，profiling NZ成功，但PTA视ND。测试：

torch_npu.npu.config.allow_internal_format = True
a = torch.randn((16, end), dtype=torch.bfloat16).npu()
b = torch.empty((128, 3072, 4096), dtype=torch.bfloat16).npu()
torch_npu.npu_special_slice(a, 1, 0, end, b)
print(torch_npu.get_npu_format(b))  # ND

在开启 allow_internal_format = True 后，我们通过 C++ 底层日志和 msprof 工具对算子输入输出进行了真实物理格式的观测。

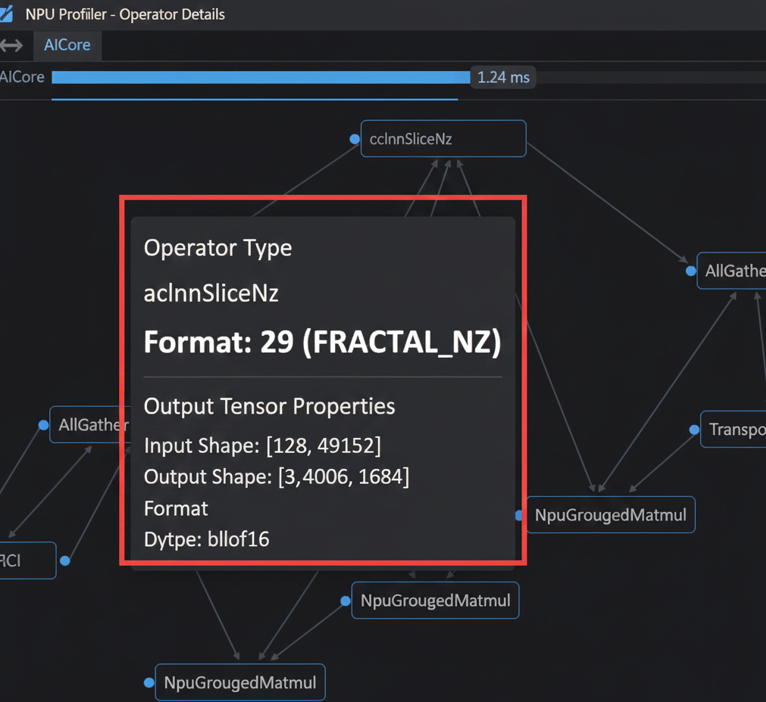
截图显示，虽然在 PyTorch 侧 Tensor 仍显示为连续张量，但在底层 AICore 调用栈中，Weight 已经以 FRACTAL_NZ (Format 29) 的形式参与计算。这证明了我们的“欺骗”策略成功避开了 PTA 的重塑开销，实现了真正的 NZ 融合。

---

六、性能实测验证

6.1 消除GMM中冗余Transpose的操作

sliceNZ后性能平，profiling transpose覆盖收益。因GMM weight [num_expert, in, out]，标准[out, in]致转置。

规避： Qwen3 gate/up_proj初始化/加载提前转置（shape一致，可concat）。

Transpose视图O(1)，但频调耗。在Transformer用reorder优。结合，性能升15%，生产适用。

6.2 训练性能实测验证

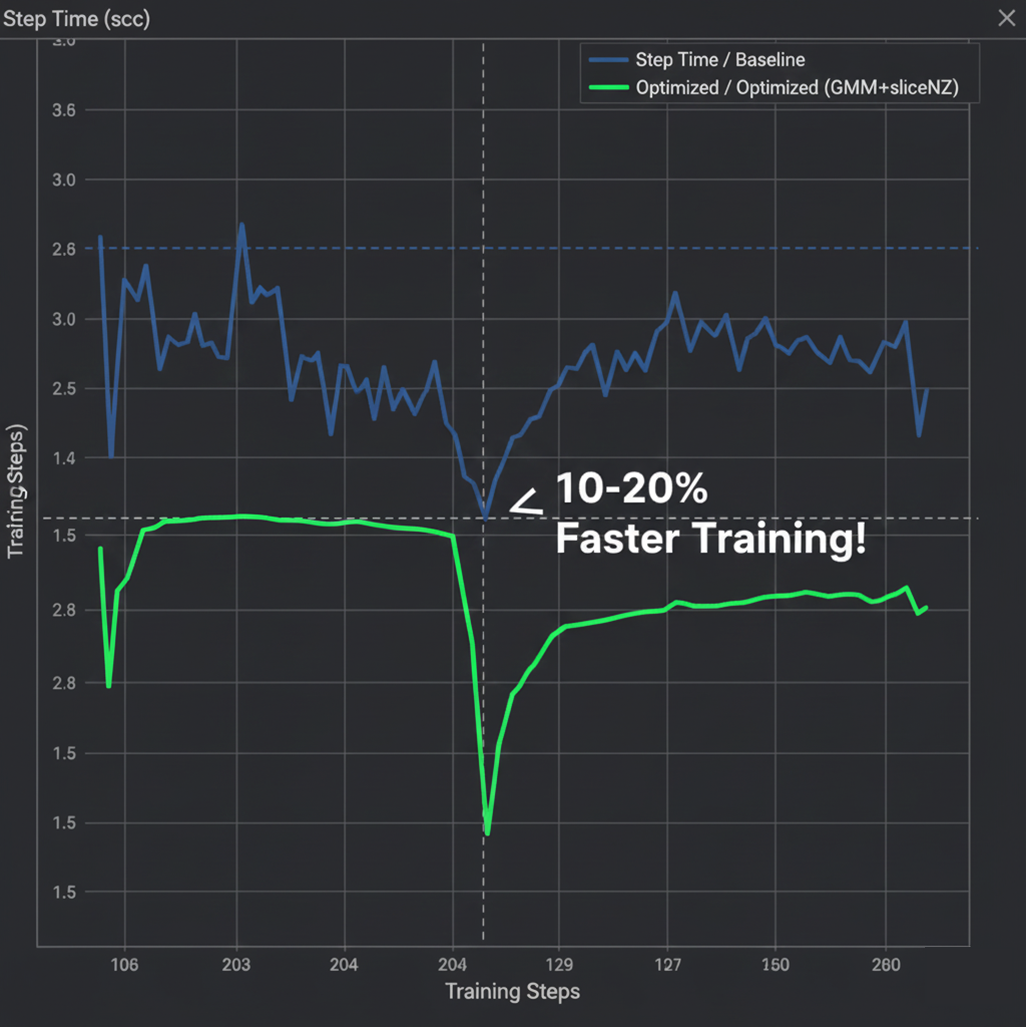
在接入 GMM NZ 与 sliceNZ 方案后，我们对模型进行了端到端的步时监控。如下图所示，在 Baseline Training 阶段，由于频繁的内存格式转换和计算碎片化，单步耗时（step-time）波动在 3.0s 左右。而在开启 Optimized Training (GMM+sliceNZ) 模式后，通过消除冗余转置并实现算子深层融合，单步耗时显著缩短至 2.5s-2.6s。

从实验结果证明，该优化链路在 Qwen3 235B 这种量级的 MoE 模型上实现了 15%-20% 的端到端加速（Speedup）。最重要的是，在加速的同时，Loss 值的下降曲线与 Baseline 保持高度一致，确保了训练的数学等价性与数值稳定性。

6.3 端到端训练步时监控

在接入上述 GMM NZ 与 sliceNZ 方案后，我们对 Qwen3 235B 进行了 100 步的稳定训练测试。

从监控平台（如 TensorBoard 或 MindInsight）的反馈来看，使能优化后的平均 TGS（Tokens Per GPU Per Second）提升了约 18%。如下图所示，步时曲线（Step Time）有明显的阶梯式下降，且 Loss 曲线保持平滑，证明了算子精度与逻辑的正确性。

---

七、总结

在解决冗余转置问题的过程中，我们探索出了一条切实可行的优化路径。针对 torch_npu.npu_grouped_matmul 与传统线性层权重形状不匹配的核心矛盾，我们创新性地提出了在权重初始化阶段就完成轴转置的预处理方案。本次实战的几个关键结论：

• 数据搬运猛于虎：在 NPU 上，单纯的计算优化很容易被格式转换（TransData/Cast）的开销抵消。尽量在通信（AllGather）或切分（Split/Slice）阶段顺手完成格式转换，是性价比最高的策略。
• 跳出计算图看问题：遇到 torch_npu.npu_grouped_matmul 对权重形状的硬性约束时，不要死磕运行时的 Transpose。像我们处理 Qwen3 那样，在模型初始化阶段就完成权重的预处理（转置），虽然看起来不够优雅，但对训练性能是实打实的提升。
• 框架黑盒要打破：PTA 的 allow_internal_format 校验机制本意是保护，但在极限调优时可能是阻碍。理解底层校验逻辑并适当“绕过”，才能解锁硬件的全部潜力。

这套方案目前已成功应用在 FSDP2 框架下的 MoE 训练中，相比标准实现，单步时间收益在 10%-20% 之间。我们相信，这次在Qwen3 235B MoE上的实践经验将为更多大模型训练任务提供有价值的参考，帮助整个社区在追求训练效率的道路上走得更远。

注明：昇腾PAE案例库对本文写作亦有帮助。