实战:手把手教你训练RNN预测函数值
本文介绍了一个使用RNN模型预测三角函数值的简单实现。文章详细说明了如何构建一个3层RNN网络,使用PyTorch的nn.RNN模块实现正弦值到余弦值的预测任务。关键点包括: 模型参数设置:input_size=1(单值输入)、hidden_size=32、num_layers=3 数据生成方法:在π范围内均匀采样300个点作为输入序列 训练过程:使用MSE损失函数和Adam优化器,加入学习率调整
前言
网上RNN的代码非常多,比如通过RNN预测房价以及股票,或者通过RNN写诗写周杰伦的歌词等,但这些代码有的是片段,有的没有提供数据集,非常麻烦。
今天用一个最简单的代码,不用去下载复杂的数据集,去预测三角函数值。首先明确一下我们的任务:我们要通过sin函数值去预测cos函数值。
比如当我们的输入为0时,sin(0)=0,cos(0)=1;
比如当我们的输入为pai/2时,sin(pai/2)=1,cos(pai/2)=0;
比如当我们的输入为pai时,sin(pai)=0,cos(pai)=-1;
因此到时候模型训练完成之后,我们模型的功能是:输入的是一个序列比如sin(0)到sin(2*pai),中间平均取300个点,输出是对应的cos值。
1、搭建RNN模型
我们给出RNN模型的torch代码:
class Rnn(nn.Module):
def __init__(self, input_size):
super(Rnn, self).__init__()
self.rnn = nn.RNN(
input_size=input_size,
hidden_size=32,
num_layers=3,
batch_first=True # 输入形状为[批量大小, 数据序列长度, 特征维度]
)
self.out = nn.Linear(32, 1)
def forward(self, x, h_0):
r_out, h_n = self.rnn(x, h_0)
outs = []
# r_out.size=[1,10,32]即将一个长度为10的序列的每个元素都映射到隐藏层上
for time in range(r_out.size(1)):
outs.append(self.out(r_out[:, time, :]))
return torch.stack(outs, dim=1), h_n
目前在torch中,已经有了RNN的模块,直接使用nn.RNN,我们介绍一下nn.RNN里面的参数。
1.1 input_size
input_size在这里是1,是因为RNN在处理序列时,序列中的每一个元素的长度并不都是1,这里input_size是1是因为我们输入的是一个sin值序列,比如我们在如sin(0)到sin(2*pai)中取300个点,每个点的值就是一个单一的数值,它的长度为1,这个1,表示的值就是input_size。
- 举例说明:
-
如果处理股价预测,每个时间步只有"价格"一个特征,则input_size=1
-
如果处理天气预测,每个时间步有"温度、湿度、气压"3个特征,则input_size=3
-
如果处理文本,每个词用100维词向量表示,则input_size=100
-
1.2 hidden_size
表示RNN隐藏状态的维度,即每个时间步输出的特征维度,可以理解为神经元个数。hidden_size=32,决定了模型的容量和学习能力,作用如下:
-
存储序列的历史信息
-
控制模型的复杂度和表达能力
-
较大的hidden_size可以学习更复杂的模式,但可能过拟合
-
典型取值:32, 64, 128, 256等(通常是2的幂次) 在文字写书写不同数量的
#可以完成不同的标题,如下:
1.3 num_layers
-
num_layers=1:单层RNN
-
num_layers>1:多层RNN(深度RNN)
-
在代码中:num_layers=3,表示有3层RNN堆叠在一起。 在这里我们一定要明确一点,平时我们看到的RNN的图实际上是一层RNN:
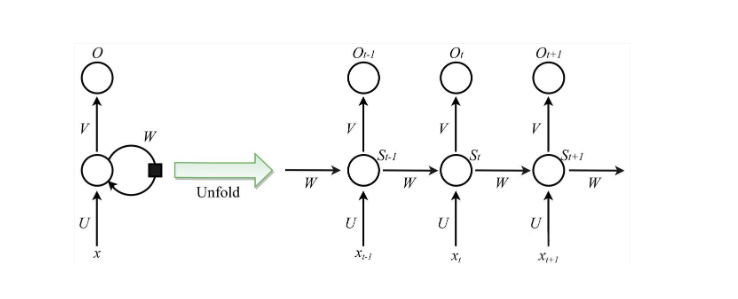
但真实的RNN其实一般不止一层,大家感兴趣的可以去看看B站梗直哥画的立体图,因此上面的图其实是下面立体图旋转九十度的正视图。此时的RNN就是3层RNN叠在一起的。
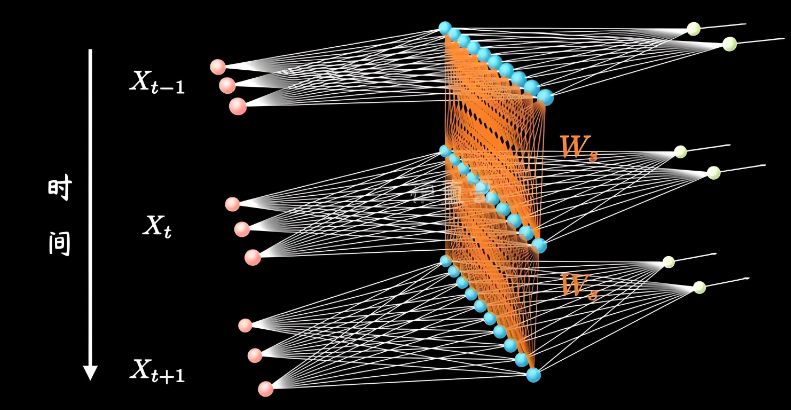
1.3 batch_first
batch_first是true还是false,事实上就是到时候你的输入数据的第一个维度是不是batch_size的大小罢了。
- batch_first=False(默认值):张量形状为 (sequence_length, batch_size, input_size)
-
序列长度在第一维
-
批次大小在第二维
-
- batch_first=True:张量形状为 (batch_size, sequence_length, input_size)
-
批次大小在第一维
-
序列长度在第二维
-
2.损失函数和优化器
loss_func = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=LR)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.5, patience=10, verbose=True)
h_state = None # 初始化h_state为None
此处使用的是均方差损失函数和亚当优化器,一般这种预测的回归任务我们都用均方差损失函数。
3.训练RNN
for step in range(500):
# 人工生成输入和输出,输入x.size=[1,10,1],输出y.size=[1,10,1]
start, end = step * np.pi, (step + 1) * np.pi
# np.linspace生成一个指定大小,指定数据区间的均匀分布序列,TIME_STEP是生成数量
steps = np.linspace(start, end, TIME_STEP, dtype=np.float32)
# print("steps", steps)
x_np = np.sin(steps)
y_np = np.cos(steps)
real_value.append(y_np.flatten())
# 从numpy.ndarray创建一个张量 np.newaxis增加新的维度
x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis])
y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])
prediction, h_state = model(x, h_state)
predict_value.append(prediction.data.numpy().flatten())
h_state = h_state.data
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss_value.append(loss.item())
loss.backward()
# 梯度裁剪 - 防止梯度爆炸
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
# 更新优化器参数
optimizer.step()
# 更新学习率
scheduler.step(loss)
3.1 构造输入数据和真实数据
steps: 每次训练我们都会构造范围为pai的数据,然后将这pai的范围平均分成30份,这每个点就是我们的steps序列啦。根据step去构造输入序列。
x_np = np.sin(steps) 和 y_np = np.cos(steps):
就是我们构造的输入数据和真实数据了,输入是sin(steps),期望输出是cos(steps)。
与此同时,我们需要适应网络的输入,刚才说到batch_first,我们通过torch.from_numpy(x_np[np.newaxis, :, np.newaxis])进行适应。
3.2 网络训练和反向传播
网络在前面构造好之后,网络训练就蛮简单的: prediction, h_state = model(x, h_state),再进行反向传播和优化器就ok了。
prediction, h_state = model(x, h_state)
predict_value.append(prediction.data.numpy().flatten())
h_state = h_state.data
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss_value.append(loss.item())
loss.backward()
4. 得到结果绘图
我们在网络训练过程中,会将真实值和预测值保存下来,同时保存loss函数,将最终结果绘图:
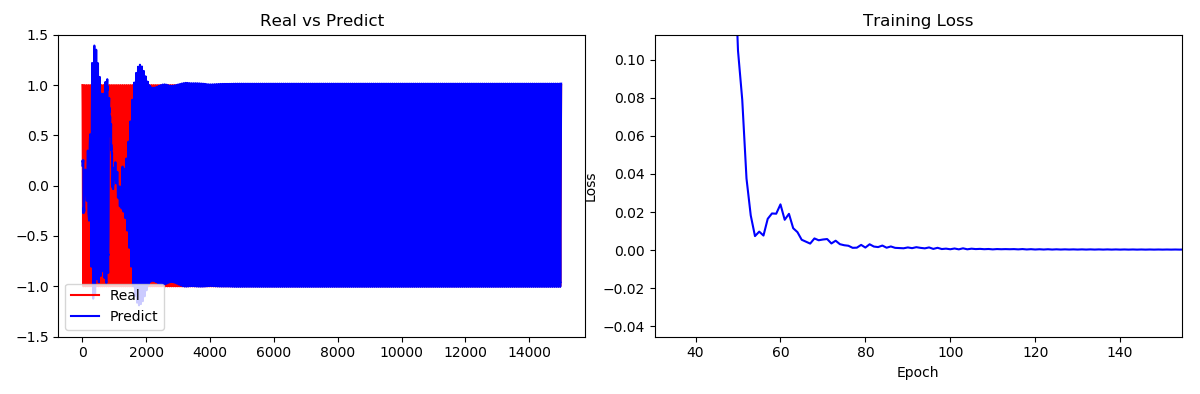
4.1 真实值和预测值对比:
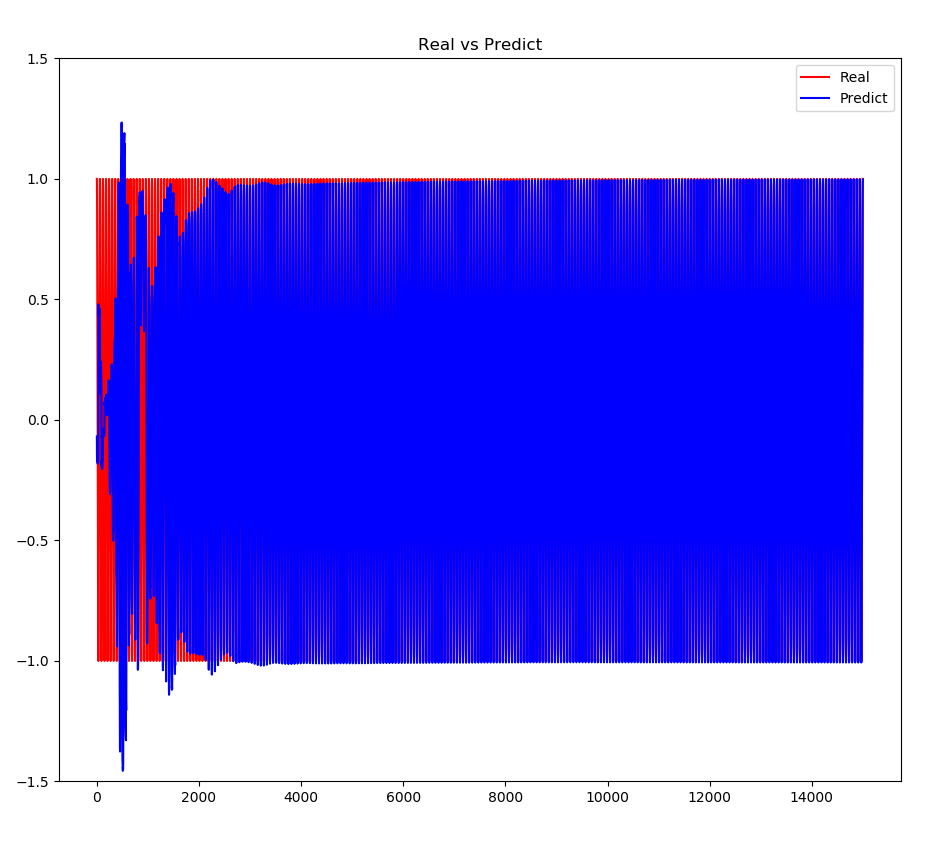
我们可以看到一开始真实值和预测值差距和还蛮大的,大概在3000左右时,真实值和预测值就很接近了。一个epoch中有30个值,因此4000次左右大概在第100epoch左右。 我们放大看看,可以看到最后真实值和预测值基本重合了:
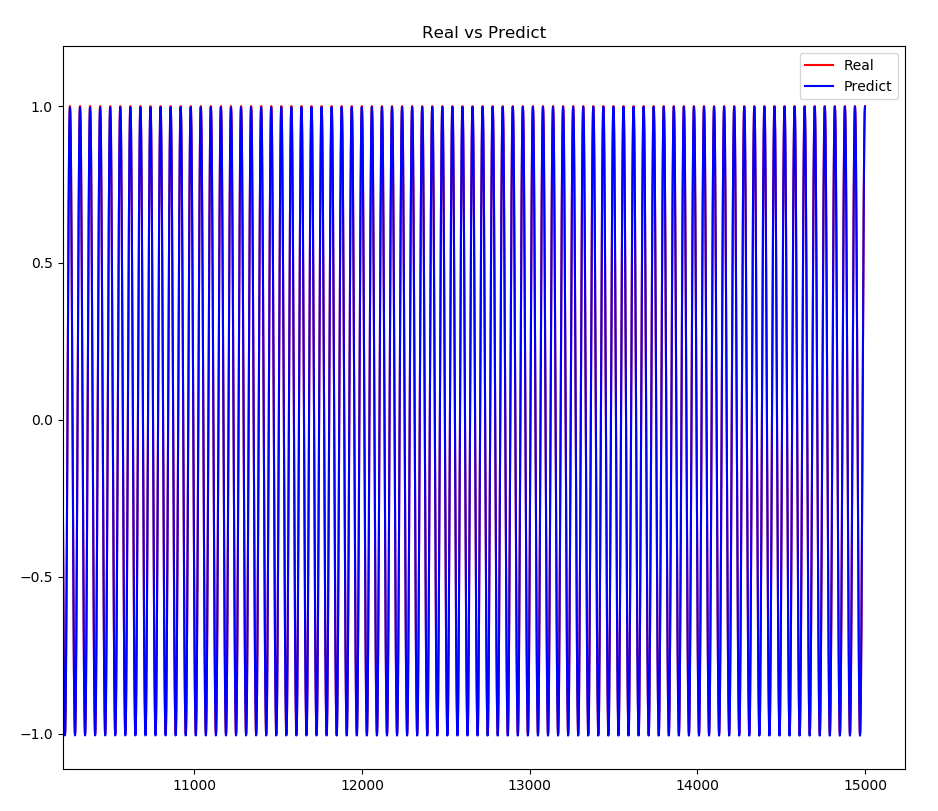
4.2 Loss曲线:
我们看到在第100个epoch时,Loss基本收敛,对应的也是真实值和预测值基本完全重合。
今天分享的RNN代码虽然简单,但是也是我不断调整出来的,一开始的代码经常会出现Loss无法收敛的情况,因此我加入了学习率优化,同时叠加了RNN的层数,最后就可以得到稳定的模型了。
大家感兴趣的也可以修改其他参数尝试调整。
由于全部代码太长,限于篇幅,就没有全部贴出,因此如果需要获取全部代码,可以关注我的gzh:阿龙AI日记,回复:项目代码
在DeepLearning-Example/项目代码/快速入门NLP中找到RNN预测余弦函数值.zip就可以下载啦。

鲲鹏昇腾开发者社区是面向全社会开放的“联接全球计算开发者,聚合华为+生态”的社区,内容涵盖鲲鹏、昇腾资源,帮助开发者快速获取所需的知识、经验、软件、工具、算力,支撑开发者易学、好用、成功,成为核心开发者。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)