🎓 一、环境配置安装

🌵 1.1 环境配置和安装

  有关环境配置和安装，以及具体gpu（如3090）上的编译错误问题，请参考博客：LeetCUDA学习记录（一）——elementwise算子代码实现详细解读

🍀 1.2 sigmoid算子运行体验

  简介：sigmoid算子通过PyTorch C++/CUDA 扩展实现 GPU 加速的直方图统计。对应仓库难度：Easy⭐️
  Sigmoid 函数是机器学习里常用的激活函数，能把任意实数输入压缩到 0 到 1 之间 —— 比如输入负数会输出接近 0 的数，输入正数会输出接近 1 的数，输入 0 时正好输出 0.5。它的核心作用是给模型输出 “概率感”，比如在二分类任务里，用 Sigmoid 输出的结果可以直接理解为 “属于某一类的概率”；同时也能让模型学到数据里的非线性关系，让复杂问题的拟合更精准。不过它也有小缺点，比如输入绝对值太大时容易出现 “梯度消失”，导致模型难训练，所以实际用的时候会结合场景和其他激活函数搭配。

  笔者使用的是3090显卡，因此需修改sigmoid.py中的配置，在extra_cuda_cflags中添加以下项：

# new add, 添加针对不同 GPU 架构的编译选项
"-gencode=arch=compute_86,code=sm_86",   # 3090

  同时由于笔者在自己的conda环境中安装的是11.7版本的cuda，因此会提示找不到sigmoid.cu的#include <cuda_fp8.h>头文件。但笔者发现在实际实现过程中，并没有用到该头文件，因此笔者注释并加入根据cuda版本的判断逻辑，可以成功运行并且不影响运行结果。

// #include <cuda_fp8.h>
#if __CUDACC_VER_MAJOR__ >= 12
#include <cuda_fp8.h>
#endif

  按照上面配置重新运行sigmoid.py程序：

CUDA_VISIBLE_DEVICES=1 python3 sigmoid.py

得到结果如下（更多结果已省略），可以看出已经正确执行：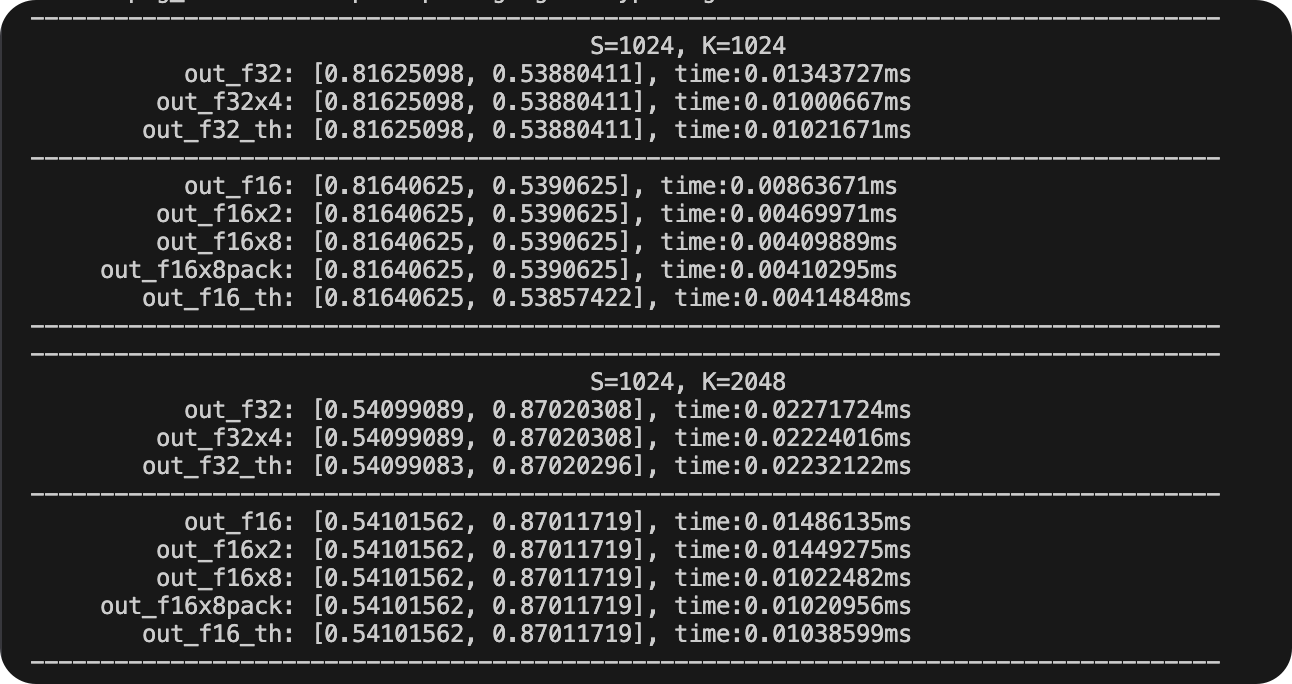

🚀 二、sigmoid算子代码解读

🏅 2.1 sigmoid算子代码结构

  整个LeetCUDA sigmoid算子包括三部分文件：

• sigmoid.py: 用 CUDA 实现了不同精度（FP32 单精度、FP16 半精度）和不同向量优化的 Sigmoid 算子核函数，还通过宏定义生成对应的 C++ 接口函数，最后绑定到 PyTorch 扩展模块，让 Python 能直接调用这些 GPU 加速的 Sigmoid 函数。
• sigmoid.cu: 加载自定义的 CUDA Sigmoid 算子模块，再定义一个基准测试函数（含预热、多次迭代计时，还会输出结果和平均耗时），接着遍历不同尺寸的输入张量（S 和 K 组合），分别对 FP32 精度和 FP16 精度（自定义基础版、2/8 元素优化版、8 元素打包优化版，以及 PyTorch 原生版）的 Sigmoid 函数做性能测试，最终输出各版本的计算结果和平均耗时，用来对比不同实现的效率。
• README.md: 代码的运行说明和运行结果。

🀄️ 2.2 sigmoid.py代码解读

🏆 2.2.1 导入模块与设置

• torch.utils.cpp_extension.load：动态编译并加载 CUDA / C++ 扩展。
• torch.set_grad_enabled(False)：关闭梯度计算，减少开销，提高性能。

import time # 用于计时
from functools import partial
from typing import Optional

import torch
from torch.utils.cpp_extension import load

torch.set_grad_enabled(False) # 全局关闭梯度计算（只做推理/性能测试时更快）

🌟 2.2.2 加载 CUDA 内核扩展

  使用 torch.utils.cpp_extension.load 将 CUDA 内核编译成 Python 可调用模块。支持不同版本直方图统计计算的内核。

• -gencode 指定 GPU 架构，以确保内核可以在对应设备上运行。
• --use_fast_math 启用快速数学运算，牺牲精度换性能。

# Load the CUDA kernel as a python module
lib = load(
    name="sigmoid_lib",
    sources=["sigmoid.cu"],  # CUDA 源文件
    extra_cuda_cflags=[
        "-O3",
        "-U__CUDA_NO_HALF_OPERATORS__",  # 启用半精度 float16 运算支持
        "-U__CUDA_NO_HALF_CONVERSIONS__",
        "-U__CUDA_NO_HALF2_OPERATORS__",
        "-U__CUDA_NO_BFLOAT16_CONVERSIONS__",
        "--expt-relaxed-constexpr",
        "--expt-extended-lambda", # 允许 CUDA lambda 扩展
        "--use_fast_math", # 使用快速数学运算（牺牲精度换速度）
        # new add, 添加针对不同 GPU 架构的编译选项
        "-gencode=arch=compute_86,code=sm_86"   # 3090
    ],
    extra_cflags=["-std=c++17"],
)

🍎 2.2.3 测试不同方法实现的算子的正确性

  代码首先定义了性能测试函数run_benchmark，核心逻辑是：先通过 “预热” 让 GPU 进入稳定状态，再多次重复执行目标函数并精确计时，最后计算平均耗时并输出关键结果。它支持两种模式（传入输出张量原地计算或函数返回新张量），能打印结果的前 2 个元素（验证计算正确性）和平均耗时（评估性能），最终目的是公平对比不同实现（如自定义优化算子与 PyTorch 原生函数）的效率。

def run_benchmark(
    perf_func: callable, # 待测试的性能函数（如自定义Sigmoid算子或PyTorch原生函数）
    x: torch.Tensor, # 输入张量（GPU上的张量，用于函数计算）
    tag: str, # 测试标签（用于区分不同版本的实现，如"f32"、"f16x4"）
    out: Optional[torch.Tensor] = None, # 输出张量（可选，用于存储计算结果，避免重复分配内存）
    warmup: int = 10, # 预热迭代次数（让GPU进入稳定状态，避免首次调用的初始化耗时影响结果）
    iters: int = 1000, # 正式计时的迭代次数（多次迭代取平均，提高时间测量精度）
    show_all: bool = False, # 是否打印完整的输出张量（默认只打印前2个元素）
):
    # 若指定了输出张量，先将其清零（避免之前的计算结果干扰）
    if out is not None:
        out.fill_(0)

    # warmup
    # 预热环节：执行多次函数调用，让GPU加载核函数、缓存数据，确保后续计时稳定
    if out is not None: # 若有输出张量，调用函数时传入out（原地修改结果）
        for i in range(warmup):
            perf_func(x, out)
    else: # 若无输出张量，直接调用函数（函数内部会返回新结果）
        for i in range(warmup):
            _ = perf_func(x)
    # 同步GPU：确保预热阶段的所有操作都已完成，再进入正式计时
    torch.cuda.synchronize()

    start = time.time() # 正式计时开始
    # iters
    # 正式迭代：多次执行函数，累积耗时
    if out is not None:
        for i in range(iters):
            perf_func(x, out)
    else:
        for i in range(iters):
            out = perf_func(x) # 若函数返回新张量，用out接收
    # 同步GPU：确保所有迭代操作完成后再停止计时，避免异步执行导致的时间误差
    torch.cuda.synchronize()
    end = time.time()
    # 计算总耗时（转换为毫秒）和平均耗时（总耗时/迭代次数）
    total_time = (end - start) * 1000  # ms
    mean_time = total_time / iters
    # 准备输出信息：标签格式化、取输出张量前2个元素（四舍五入到8位小数）
    out_info = f"out_{tag}"
    out_val = out.flatten().detach().cpu().numpy().tolist()[:2]
    out_val = [round(v, 8) for v in out_val]
    # 打印结果：对齐标签、输出前2个元素值、平均耗时
    print(f"{out_info:>18}: {out_val}, time:{mean_time:.8f}ms")
    # 若需要，打印完整的输出张量
    if show_all:
        print(out)
    return out, mean_time # 返回输出张量和平均耗时（供后续分析或对比）

  接着代码通过不同尺寸的具体张亮对比不同版本 Sigmoid 函数的性能。代码首先定义了 9 种不同大小的二维张量（从 1024×1024 到 4096×4096），然后对每种尺寸分别测试两种精度（FP32 单精度、FP16 半精度）下的多个 Sigmoid 实现 —— 包括自定义的基础版、向量优化版（如一次处理 4 个或 8 个元素），以及 PyTorch 原生函数。通过调用性能测试函数，输出每种实现的计算结果（前两个值）和平均耗时，以此直观对比不同优化方式（向量计算、精度调整）对 Sigmoid 运算效率的影响。

# 遍历所有尺寸组合，对每种尺寸进行性能测试
for S, K in SKs:
    print("-" * 85)
    print(" " * 40 + f"S={S}, K={K}")
    # 生成FP32精度的输入张量：
    # 形状为(S, K)，随机值（符合标准正态分布），存储在GPU上，且内存连续（优化访问速度）
    x = torch.randn((S, K)).cuda().float().contiguous()
    # 生成与输入同形状、同精度的输出张量（用于存储计算结果，避免重复分配内存）
    y = torch.zeros_like(x).cuda().float().contiguous()
    # 测试FP32精度的3种Sigmoid实现：
    # 1. 自定义基础版（单元素处理）
    run_benchmark(lib.sigmoid_f32, x, "f32", y)
    # 2. 自定义SIMD优化版（4元素并行处理）
    run_benchmark(lib.sigmoid_f32x4, x, "f32x4", y)
    # 3. PyTorch原生版（用partial固定输出张量，确保原地计算）
    run_benchmark(partial(torch.sigmoid, out=y), x, "f32_th")

    print("-" * 85)
    # 将输入和输出张量转换为FP16精度（半精度），并确保内存连续
    x_f16 = x.half().contiguous()
    y_f16 = y.half().contiguous()
    # 测试FP16精度的5种Sigmoid实现：
    # 1. 自定义基础版（单元素处理）
    run_benchmark(lib.sigmoid_f16, x_f16, "f16", y_f16)
    # 2. 自定义SIMD优化版（2元素并行处理）
    run_benchmark(lib.sigmoid_f16x2, x_f16, "f16x2", y_f16)
    # 3. 自定义SIMD优化版（8元素并行处理）
    run_benchmark(lib.sigmoid_f16x8, x_f16, "f16x8", y_f16)
    # 4. 自定义打包优化版（8元素打包处理，进一步优化内存访问）
    run_benchmark(lib.sigmoid_f16x8_pack, x_f16, "f16x8pack", y_f16)
    # 5. PyTorch原生版（固定输出张量，原地计算）
    run_benchmark(partial(torch.sigmoid, out=y_f16), x_f16, "f16_th")
    print("-" * 85)

🌕 2.3 sigmoid.cu代码解读

⚡️ 2.3.1 头文件和宏定义

  这段代码是 GPU 加速计算的 “基础工具包”，主要定义了适配不同数据类型（如整数、单精度浮点 FP32、半精度浮点 FP16/BF16）的向量操作宏，以及数值计算中防止溢出的范围常量。它通过宏定义将连续内存中的多个数据打包成 GPU 支持的向量类型（如 4 个 float 打包成 float4），方便后续核函数用 SIMD（单指令多数据）方式并行处理，提升计算效率；同时定义了不同精度下指数函数的安全输入范围，避免计算时出现数值溢出问题。这些定义为后续实现高效的 Sigmoid GPU 算子打下了基础，让代码既能适配多种数据精度，又能充分利用 GPU 的向量计算能力。

// 引入标准算法库，提供基础算法支持（如max、min等）
#include <algorithm>
// 引入CUDA的bfloat16数据类型支持（用于半精度浮点计算）
#include <cuda_bf16.h>
// 引入CUDA的FP16（half）数据类型支持（半精度浮点计算）
#include <cuda_fp16.h>
// 注释：FP8数据类型支持（当前未启用，预留扩展）
// #include <cuda_fp8.h>
// 条件编译：若CUDA编译器版本>=12，启用FP8数据类型支持（新一代硬件支持更低精度计算）
#if __CUDACC_VER_MAJOR__ >= 12
#include <cuda_fp8.h>
#endif
// 引入CUDA运行时API，用于GPU内存管理、核函数调用等底层操作
#include <cuda_runtime.h>
// 引入浮点数常量定义（如FLT_MAX，用于数值范围限制）
#include <float.h>
// 引入标准输入输出库，用于调试打印
#include <stdio.h>
// 引入标准库，提供动态内存分配等功能
#include <stdlib.h>
// 引入PyTorch C++扩展接口，用于与PyTorch张量交互
#include <torch/extension.h>
// 引入PyTorch类型定义，包含张量类型等基础定义
#include <torch/types.h>
// 引入向量容器库，用于动态数组操作
#include <vector>

// 宏定义：GPU的warp大小（NVIDIA GPU的基本执行单元，一个warp含32个线程）
#define WARP_SIZE 32
// 宏定义：将内存地址指向的4个连续int元素转换为int4向量类型（CUDA原生4元素整数向量）
// 用于SIMD优化，一次处理4个整数
#define INT4(value) (reinterpret_cast<int4 *>(&(value))[0])
// 宏定义：将内存地址指向的4个连续float元素转换为float4向量类型（CUDA原生4元素浮点向量）
// 用于FP32精度的SIMD优化，一次加载/处理4个单精度浮点数
#define FLOAT4(value) (reinterpret_cast<float4 *>(&(value))[0])
// 宏定义：将内存地址指向的2个连续half元素转换为half2向量类型（CUDA原生2元素半精度向量）
// 用于FP16精度的SIMD优化，一次加载/处理2个半精度浮点数
#define HALF2(value) (reinterpret_cast<half2 *>(&(value))[0])
// 宏定义：将内存地址指向的2个连续bfloat16元素转换为__nv_bfloat162向量类型
// 用于BF16精度的SIMD优化，一次加载/处理2个bfloat16浮点数
#define BFLOAT2(value) (reinterpret_cast<__nv_bfloat162 *>(&(value))[0])
// 宏定义：将内存地址指向的16字节（128位）数据转换为float4向量类型
// 用于优化内存访问，一次加载/存储128位数据（提升内存带宽利用率）
#define LDST128BITS(value) (reinterpret_cast<float4 *>(&(value))[0])
// 宏定义：FP32精度下exp函数的最大输入值（超过此值时exp输出会溢出，需截断）
#define MAX_EXP_F32 88.3762626647949f
// 宏定义：FP32精度下exp函数的最小输入值（低于此值时exp输出接近0，需截断）
#define MIN_EXP_F32 -88.3762626647949f
// 宏定义：FP16精度下exp函数的最大输入值（转为half类型，避免溢出）
#define MAX_EXP_F16 __float2half(11.089866488461016f)
// 宏定义：FP16精度下exp函数的最小输入值（half类型，避免输出过小）
#define MIN_EXP_F16 __float2half(-9.704060527839234f)

这里#define INT4(value)把某个变量 reinterpret 为 int4 类型指针，然后取第一个 int4。

#define INT4(value) (reinterpret_cast<int4 *>(&(value))[0])

解释：int4 是 CUDA 提供的 4 个 int 的向量类型（4 × 32-bit = 128-bit）。reinterpret_cast<int4 *>(&(value))：将变量的地址视为 int4。[0]：访问这个向量。
用途：用于向量化加载/存储 4 个 int，一次操作 128-bit，提高内存吞吐量。比如：

int data[4] = {1,2,3,4};
int4 vec = INT4(data);  // 将 data 当作 int4 使用

📉 2.3.3 FP32 类型Sigmoid算子的 CUDA 核函数实现

🎑 2.3.3.1 基础版（单元素处理）FP32 类型Sigmoid算子的 CUDA 核函数实现（sigmoid_f32_kernel）

  这段代码是在 GPU 上计算单精度浮点数（FP32）Sigmoid 函数的核心核函数。它通过 “一个线程处理一个数据” 的方式并行计算：先给每个线程分配唯一的全局索引，让线程对应输入数组的一个元素；接着读取元素值并截断到安全范围（避免计算溢出）；最后代入 Sigmoid 公式算出结果并写入输出数组。同时通过线程索引检查防止越界，线程配置（256 线程 / 块）也适配了 GPU 硬件特性，能高效利用 GPU 的并行算力。

功能：Sigmoid算子的CUDA核函数（针对fp32类型数据）

• grid(N/256)：网格维度设置为输入数据量N除以256（每个网格包含若干线程块）
• block(256)：线程块维度为256（每个线程块包含256个线程）

参数说明：

• x: 输入数组（存放输入数据）
• y: 输出数组（存放Sigmoid函数计算后结果）
• N: 输入数组x的元素总数

// 标注当前核函数针对FP32（单精度浮点数）数据类型
// Sigmoid函数数学定义：输入为长度N的数组x，输出为长度N的数组y，满足y[i] = 1/(1+exp(-x[i]))
// 核函数的GPU线程配置说明：
//   grid(N/256)：网格（grid）维度按输入数据量N除以256设置（每个网格包含多个线程块）
//   block(K=256)：线程块（block）维度固定为256（每个线程块包含256个并行线程）
// FP32
// Sigmoid x: N, y: N y=1/(1+exp(-x))
// grid(N/256), block(K=256)
__global__ void sigmoid_f32_kernel(float *x, float *y, int N) {
  // 计算当前线程的“全局索引”：定位线程在所有线程中的唯一位置
  // 公式含义：线程块在网格中的索引 × 块内线程数 + 线程在块内的索引
  int idx = blockIdx.x * blockDim.x + threadIdx.x;
  // 线程安全检查：仅当全局索引小于输入数据总量N时才执行计算
  // 避免因线程总数（网格×线程块）略大于N导致的数组越界访问
  if (idx < N) {
    // 从GPU全局内存中读取输入数组x在当前索引处的值，存入寄存器v（寄存器访问速度远快于全局内存）
    float v = x[idx];
    // 数值范围截断：用fminf和fmaxf将v限制在[MIN_EXP_F32, MAX_EXP_F32]之间
    // 目的：防止后续expf(-v)计算溢出（v过大时expf(-v)接近0，v过小时expf(-v)溢出）
    v = fminf(fmaxf(v, MIN_EXP_F32), MAX_EXP_F32);
    // 计算Sigmoid函数值：代入公式y = 1/(1 + exp(-v))
    // expf是CUDA的单精度指数函数，计算结果存入输出数组y的对应位置
    y[idx] = 1.0f / (1.0f + expf(-v));
  }
}

👼 2.3.3.2 SIMD优化版（4元素并行处理）FP32 类型Sigmoid算子的 CUDA 核函数实现

  这段代码是单精度浮点数（FP32）Sigmoid 函数的向量优化版本，核心是让一个 GPU 线程同时处理 4 个元素。它通过向量操作一次性加载 4 个连续的输入数据到寄存器，批量完成数值范围截断和 Sigmoid 计算，再一次性将 4 个结果写回内存。线程配置上，每个线程块包含 64 个线程（是基础版的 1/4），保证总处理能力不变但内存访问效率更高。这种 “一次处理 4 个元素” 的方式充分利用了 GPU 的向量计算能力，比单个元素逐个处理更快。

功能：Sigmoid算子的CUDA核函数（针对fp32类型数据）

• grid(N/256)：网格维度设置为输入数据量N除以256（每个网格包含若干线程块）
• block(256)：线程块维度为256（每个线程块包含256个线程）

参数说明：

• x: 输入数组（存放输入数据）
• y: 输出数组（存放Sigmoid函数计算后结果）
• N: 输入数组x的元素总数

// Sigmoid函数的向量优化版本（Vec4）：输入为长度N的数组x，输出为长度N的数组y，满足y[i] = 1/(1+exp(-x[i]))
// 核函数的GPU线程配置说明：
//   grid(N/256)：网格（grid）维度按输入数据量N除以256设置（与基础版保持一致的总计算规模）
//   block(256/4)：线程块（block）维度为64（256除以4，因每个线程处理4个元素，匹配GPU算力）
// Sigmoid x: N, y: N y=1/(1+exp(-x)) Vec4
// grid(N/256), block(256/4)
__global__ void sigmoid_f32x4_kernel(float *x, float *y, int N) {
  // 计算当前线程的“基索引”：每个线程处理4个连续元素，故索引需×4
  // 公式含义：线程块索引×块内线程数（64） + 线程块内索引 → 得到线程处理的“4元素组编号”，再×4得到首个元素的全局索引
  int idx = (blockIdx.x * blockDim.x + threadIdx.x) * 4;

  // 向量加载：将x数组中从idx开始的4个连续float元素，通过FLOAT4类型一次性加载到寄存器reg_x中
  // 相比基础版的4次单独加载，向量加载减少内存访问次数，提升内存效率
  float4 reg_x = FLOAT4(x[idx]);
  float4 reg_y;

  // 对向量的4个分量量（x、y、z、w）分别进行数值值范围截断：限制在[MIN_EXP_F32, MAX_EXP_F32]之间
  // 防止后续expf计算溢出，与基础版逻辑一致，但批量处理4个元素
  reg_x.x = fminf(fmaxf(reg_x.x, MIN_EXP_F32), MAX_EXP_F32);
  reg_x.y = fminf(fmaxf(reg_x.y, MIN_EXP_F32), MAX_EXP_F32);
  reg_x.z = fminf(fmaxf(reg_x.z, MIN_EXP_F32), MAX_EXP_F32);
  reg_x.w = fminf(fmaxf(reg_x.w, MIN_EXP_F32), MAX_EXP_F32);

  // 对向量的4个分量分别计算Sigmoid值，存入reg_y的对应分量
  // 一次性完成4个元素的公式计算（y = 1/(1 + exp(-v))）
  reg_y.x = 1.0f / (1.0f + expf(-reg_x.x));
  reg_y.y = 1.0f / (1.0f + expf(-reg_x.y));
  reg_y.z = 1.0f / (1.0f + expf(-reg_x.z));
  reg_y.w = 1.0f / (1.0f + expf(-reg_x.w));

  // 索引检查：确保当前处理的首个元素不越界（避免写入出N范围的内存写入）
  if ((idx + 0) < N) {
    // 向量存储：将reg_y中的4个结果一次性写入y数组从idx开始的位置
    // 相比4次单独存储，减少内存访问次数，提升效率
    FLOAT4(y[idx]) = reg_y;
  }
}

为什么idx要*4？ FLOAT4 会把连续的 4 个元素当作一个向量处理。乘 4 是为了确保每个线程负责的 4 个元素不重叠。

#define FLOAT4(value) (reinterpret_cast<float4 *>(&(value))[0])

  举例说明（thread=0，1，2）：

thread	处理元素	x4后idx	处理元素
0	a[0:3]	0	a[0:3]
1	a[1:4]	4	a[4:7]
2	a[2:5]	8	a[8:11]

🔢 2.3.4 FP16 类型Sigmoid算子的 CUDA 核函数实现

✨ 2.3.4.1 基础版（单元素处理）FP16 类型Sigmoid算子的 CUDA 核函数实现（sigmoid_f16_kernel）

  这段代码是在 GPU 上计算半精度浮点数（FP16）Sigmoid 函数的核函数，核心是适配半精度数据的特性做高效计算。它让每个线程处理一个半精度元素：先通过线程索引定位到要处理的元素，再把元素值截断到安全范围（避免计算溢出），最后用半精度专用的指数函数（hexp）和常量，代入 Sigmoid 公式算出结果并写入输出数组。整个过程针对半精度数据优化了函数和常量类型，在保证计算正确的同时，比单精度计算更节省 GPU 内存、提升处理速度。

fp16类型Sigmoid算子的CUDA核函数
参数说明：

• x: 输入数组
• y: 输出数组
• N: 输入数组x的元素总数

//  FP16
__global__ void sigmoid_f16_kernel(half *x, half *y, int N) {
  // 计算当前线程的全局索引：线程块索引×块内线程数 + 线程在块内的索引
  // 每个线程通过该索引对应输入数组x中的一个半精度元素，实现“单线程处理单元素”
  int idx = blockIdx.x * blockDim.x + threadIdx.x;

  // 定义半精度常量1.0：通过__float2half函数将CPU端的float型1.0转换为GPU支持的half型
  // 半精度计算需使用对应精度的常量，避免类型转换误差
  const half f = __float2half(1.0f);

  // 线程安全检查：仅当索引小于输入数据总量N时执行计算，防止数组越界访问
  if (idx < N) {
    // 从GPU全局内存读取输入数组x在当前索引处的半精度值，存入寄存器v（寄存器访问速度远快于全局内存）
    half v = x[idx];
    // 将v限制在[MIN_EXP_F16, MAX_EXP_F16]之间，避免后续hexp函数计算时出现溢出或数值下溢
    v = __hmin(__hmax(v, MIN_EXP_F16), MAX_EXP_F16);
    // 计算半精度Sigmoid值：代入公式 y = 1/(1 + exp(-v))
    // hexp是CUDA内置的半精度指数函数，专门处理half类型的指数计算，确保精度和效率
    y[idx] = f / (f + hexp(-v));
  }
}

🥦 2.3.4.2 SIMD优化版（2元素并行处理）FP16 类型Sigmoid算子的 CUDA 核函数实现（sigmoid_f16x2_kernel）

  这段代码是半精度浮点数（FP16）Sigmoid 的 “2 元素并行优化版”，核心是让 1 个 GPU 线程同时处理 2 个半精度元素。它先通过向量操作一次性加载 2 个连续的输入数据到寄存器，批量完成数值截断（防止溢出）和 Sigmoid 计算，再一次性把 2 个结果写回内存。相比 “1 线程处理 1 元素” 的基础版，这种方式减少了内存访问次数，充分利用 GPU 的向量计算能力，在节省线程资源的同时，让半精度 Sigmoid 计算更快。

fp16类型Sigmoid算子的CUDA核函数（2元素并行处理）
参数说明：

• x: 输入数组
• y: 输出数组
• N: 输入数组x的元素总数

// 针对FP16（半精度浮点数）的Sigmoid向量优化核函数（x2表示1个线程处理2个元素）
// 功能：输入长度为N的half数组x，输出长度为N的half数组y，满足y[i] = 1/(1+exp(-x[i]))
__global__ void sigmoid_f16x2_kernel(half *x, half *y, int N) {
  // 计算当前线程的“基索引”：每个线程处理2个连续元素，故索引需×2
  // 公式含义：线程块索引×块内线程数 + 线程块内索引 → 得到“2元素组编号”，再×2得到首个元素的全局索引
  int idx = (blockIdx.x * blockDim.x + threadIdx.x) * 2;
  // 定义半精度常量1.0：通过__float2half将float型1.0转为GPU支持的half型，避免类型转换误差
  const half f = __float2half(1.0f);
  // 向量加载：通过HALF2宏，将x数组中从idx开始的2个连续half元素，一次性加载为half2向量类型存入寄存器reg_x
  // 相比单元素加载，减少1次内存访问，提升内存带宽利用率
  half2 reg_x = HALF2(x[idx]);
  half2 reg_y;
  // 对half2向量的两个分量（x、y）分别做数值范围截断
  // 使用半精度专用函数__hmin/__hmax，将分量限制在[MIN_EXP_F16, MAX_EXP_F16]，防止后续hexp计算溢出
  reg_x.x = __hmin(__hmax(reg_x.x, MIN_EXP_F16), MAX_EXP_F16);
  reg_x.y = __hmin(__hmax(reg_x.y, MIN_EXP_F16), MAX_EXP_F16);

  // 对两个分量分别计算Sigmoid值：代入公式 y = 1/(1 + exp(-v))
  // 使用半精度专用指数函数hexp，确保计算精度和效率，结果存入reg_y对应分量
  reg_y.x = f / (f + hexp(-reg_x.x));
  reg_y.y = f / (f + hexp(-reg_x.y));

  if ((idx + 0) < N) {
    // 向量存储：通过HALF2宏，将reg_y中的2个结果一次性写入y数组从idx开始的位置
    // 相比单元素存储，减少1次内存访问，提升效率
    HALF2(y[idx]) = reg_y;
  }
}

🥒 2.3.4.3 SIMD优化版（8元素并行处理）FP16 类型Sigmoid算子的 CUDA 核函数实现（sigmoid_f16x8_kernel）

  这段代码是半精度浮点数（FP16）Sigmoid 的 “8 元素并行优化版”，核心是让 1 个 GPU 线程一次处理 8 个半精度元素。它把 8 个元素拆成 4 组，每组 2 个元素，用 half2 向量操作批量加载到寄存器；接着逐个对 8 个元素做数值截断（防溢出）、算 Sigmoid 值；最后再分 4 组批量写回结果，还单独检查每组索引避免越界。相比 1 个线程处理 1 个或 2 个元素，这种方式能更充分利用 GPU 的向量计算能力和内存带宽，让半精度 Sigmoid 的计算效率更高。

fp16类型Sigmoid算子的CUDA核函数（8元素并行处理）
参数说明：

• x: 输入数组
• y: 输出数组
• N: 输入数组x的元素总数

// unpack f16x8
// 半精度（FP16）Sigmoid的8元素并行优化核函数（unpack表示通过多个half2向量拆分处理8元素）
// 功能：输入长度为N的half数组x，输出长度为N的half数组y，每个元素满足Sigmoid公式y[i] = 1/(1+exp(-x[i]))
__global__ void sigmoid_f16x8_kernel(half *x, half *y, int N) {
  // 计算当前线程的“基索引”：每个线程处理8个连续元素，故索引需×8
  // 公式含义：线程块索引×块内线程数 + 线程块内索引 → 得到“8元素组编号”，再×8得到首个元素的全局索引
  int idx = (blockIdx.x * blockDim.x + threadIdx.x) * 8;
  // 定义半精度常量1.0：通过__float2half将CPU端float型1.0转为GPU支持的half型，避免类型转换误差
  const half f = __float2half(1.0f);

  // 分4次加载8个半精度元素：每次通过HALF2宏加载2个连续元素，存入4个half2向量寄存器
  // 对应加载x[idx]&x[idx+1]、x[idx+2]&x[idx+3]、x[idx+4]&x[idx+5]、x[idx+6]&x[idx+7]
  half2 reg_x_0 = HALF2(x[idx + 0]);
  half2 reg_x_1 = HALF2(x[idx + 2]);
  half2 reg_x_2 = HALF2(x[idx + 4]);
  half2 reg_x_3 = HALF2(x[idx + 6]);

  // 对4个half2向量的8个分量（每个向量含x、y两个分量）逐个做数值范围截断
  // 使用半精度专用函数__hmin/__hmax，将分量限制在[MIN_EXP_F16, MAX_EXP_F16]，防止后续hexp计算溢出
  reg_x_0.x = __hmin(__hmax(reg_x_0.x, MIN_EXP_F16), MAX_EXP_F16);
  reg_x_0.y = __hmin(__hmax(reg_x_0.y, MIN_EXP_F16), MAX_EXP_F16);
  reg_x_1.x = __hmin(__hmax(reg_x_1.x, MIN_EXP_F16), MAX_EXP_F16);
  reg_x_1.y = __hmin(__hmax(reg_x_1.y, MIN_EXP_F16), MAX_EXP_F16);
  reg_x_2.x = __hmin(__hmax(reg_x_2.x, MIN_EXP_F16), MAX_EXP_F16);
  reg_x_2.y = __hmin(__hmax(reg_x_2.y, MIN_EXP_F16), MAX_EXP_F16);
  reg_x_3.x = __hmin(__hmax(reg_x_3.x, MIN_EXP_F16), MAX_EXP_F16);
  reg_x_3.y = __hmin(__hmax(reg_x_3.y, MIN_EXP_F16), MAX_EXP_F16);

  // 定义4个half2向量寄存器，用于存储8个元素的Sigmoid计算结果
  half2 reg_y_0, reg_y_1, reg_y_2, reg_y_3;

  // 对8个分量逐个计算Sigmoid值：代入公式y = 1/(1 + exp(-v))
  // 使用半精度专用指数函数hexp处理half类型，结果存入对应reg_y向量的分量
  reg_y_0.x = f / (f + hexp(-reg_x_0.x));
  reg_y_0.y = f / (f + hexp(-reg_x_0.y));
  reg_y_1.x = f / (f + hexp(-reg_x_1.x));
  reg_y_1.y = f / (f + hexp(-reg_x_1.y));
  reg_y_2.x = f / (f + hexp(-reg_x_2.x));
  reg_y_2.y = f / (f + hexp(-reg_x_2.y));
  reg_y_3.x = f / (f + hexp(-reg_x_3.x));
  reg_y_3.y = f / (f + hexp(-reg_x_3.y));

  // 分4次存储8个结果：每次通过HALF2宏存储2个元素，且单独检查索引避免越界
  // 分别存储到y[idx]&y[idx+1]、y[idx+2]&y[idx+3]、y[idx+4]&y[idx+5]、y[idx+6]&y[idx+7]
  if ((idx + 0) < N) {
    HALF2(y[idx + 0]) = reg_y_0;
  }
  if ((idx + 2) < N) {
    HALF2(y[idx + 2]) = reg_y_1;
  }
  if ((idx + 4) < N) {
    HALF2(y[idx + 4]) = reg_y_2;
  }
  if ((idx + 6) < N) {
    HALF2(y[idx + 6]) = reg_y_3;
  }
}

🥔 2.3.4.4 SIMD优化版（8元素打包处理，进一步优化内存访问）FP16 类型Sigmoid算子的 CUDA 核函数实现（sigmoid_f16x8_pack_kernel）

  这段代码是半精度浮点数（FP16）Sigmoid 的 “8 元素打包优化版”，核心是用 128 位打包方式进一步提升内存访问效率。它让 1 个 GPU 线程处理 8 个半精度元素：先通过 1 次 128 位内存访问，把 8 个元素一次性加载到临时数组；再用循环展开优化，并行完成 8 个元素的数值截断和 Sigmoid 计算；最后在确认不越界的情况下，通过 1 次 128 位访问把 8 个结果批量写回。相比拆分加载 / 存储的版本，这种 “1 次加载 8 个、1 次存储 8 个” 的打包方式，最大限度减少了内存访问次数，让 GPU 算力更充分发挥，计算速度更快。

fp16类型Sigmoid算子的CUDA核函数（8元素打包处理，进一步优化内存访问）
参数说明：

• x: 输入数组
• y: 输出数组
• N: 输入数组x的元素总数

// pack f16x8
// 半精度（FP16）Sigmoid的8元素打包优化核函数（pack表示用128位打包方式加载/存储8个元素）
// 功能：输入长度为N的half数组x，输出长度为N的half数组y，每个元素满足Sigmoid公式y[i] = 1/(1+exp(-x[i]))
__global__ void sigmoid_f16x8_pack_kernel(half *x, half *y, int N) {
  // 计算当前线程的“基索引”：每个线程处理8个连续元素，故索引需×8
  // 公式含义：线程块索引×块内线程数 + 线程块内索引 → 得到“8元素组编号”，再×8得到首个元素的全局索引
  int idx = (blockIdx.x * blockDim.x + threadIdx.x) * 8;

  // 定义半精度常量1.0：通过__float2half将CPU端float型1.0转为GPU支持的half型，避免类型转换误差
  const half f = __float2half(1.0f);

  // temporary register(memory), .local space in ptx, addressable
  // 定义两个半精度数组作为临时寄存器：pack_x存输入的8个元素，pack_y存计算结果
  // 8个half元素共128位（8×16bit），适配GPU的128位内存访问粒度
  half pack_x[8], pack_y[8]; // 8x16 bits=128 bits.

  // reinterpret as float4 and load 128 bits in 1 memory issue.
  // 128位打包加载：通过LDST128BITS宏，将x数组中从idx开始的128位数据（即8个half元素）
  // 以float4类型（128位）一次性加载到pack_x数组起始位置，仅需1次内存访问
  // reinterpret as float4 and load 128 bits in 1 memory issue.
  LDST128BITS(pack_x[0]) = LDST128BITS(x[idx]); // load 128 bits

  // 循环展开优化：#pragma unroll 指令让编译器将循环展开为8次独立操作
  // 避免循环控制开销，同时让8个元素的计算能并行执行，提升效率
#pragma unroll
  for (int i = 0; i < 8; ++i) {
    // 对每个元素做数值范围截断：用__hmin/__hmax限制在[MIN_EXP_F16, MAX_EXP_F16]，防止hexp溢出
    half v = __hmin(__hmax(pack_x[i], MIN_EXP_F16), MAX_EXP_F16);
    // 计算Sigmoid值，结果存入pack_y对应位置
    pack_y[i] = f / (f + hexp(-v));
  }
  
  // reinterpret as float4 and store 128 bits in 1 memory issue.
  // 128位打包存储：仅当当前8元素组的最后一个元素（idx+7）未越界时，
  // 通过LDST128BITS宏将pack_y中的128位数据（8个结果）一次性写入y数组，仅需1次内存访问
  // reinterpret as float4 and store 128 bits in 1 memory issue.
  if ((idx + 7) < N) {
    LDST128BITS(y[idx]) = LDST128BITS(pack_y[0]);
  }
}

🦭 2.3.5 把 CUDA kernel 封装成 PyTorch 可调用的扩展函数

  剩余代码主要是将不同版本的 CUDA histogram kernel封装成 PyTorch 扩展函数，并通过 PyBind11 注册到 Python 中。
核心代码主要是以下内容：

1. 用 TORCH_BINDING_ELEM_ADD 自动生成一系列 C++ 封装函数。
2. 用 PYBIND11_MODULE 和 m.def把这些函数绑定到 Python模块里。
3. 最终，Python 可以直接调用这些扩展函数，而内部会执行高性能 CUDA 内核。

// 宏定义1：将输入的标识符转换为字符串（例如把func转为"func"）
// 用于后续绑定函数时，统一函数名的字符串表示
#define STRINGFY(str) #str
// 宏定义2：通用的PyTorch函数绑定宏
// 功能：将C++函数func绑定到PyTorch模块m中，函数名（字符串形式）与函数本身同名
// 作用：简化多个函数的重复绑定代码，避免手动写重复的def调用
#define TORCH_BINDING_COMMON_EXTENSION(func)                                   \
  m.def(STRINGFY(func), &func, STRINGFY(func));

// 宏定义3：PyTorch张量数据类型检查宏
// 功能：检查张量T的数据类型是否等于指定的th_type
// 若不匹配：打印张量当前的类型信息，并抛出运行时错误（提示需使用th_type类型）
#define CHECK_TORCH_TENSOR_DTYPE(T, th_type)                                   \
  if (((T).options().dtype() != (th_type))) {                                  \
    std::cout << "Tensor Info:" << (T).options() << std::endl;                 \
    throw std::runtime_error("values must be " #th_type);                      \
  }

  这个宏是生成 Sigmoid 函数 C++ 接口的 “自动化工具”，核心是根据不同参数批量生成适配不同精度、不同优化版本的接口函数，同时智能配置 GPU 线程。它先检查输入输出张量的数据类型是否正确，再根据张量维度（是否为 2 维）和特征数大小，分三种情况配置线程块和网格：非 2 维张量按 “总元素数” 分配线程，2 维张量若特征数适中则按 “样本级” 并行（每个线程块处理 1 个样本），特征数过大则退化为 “总元素数” 模式。最后调用对应的 CUDA 核函数完成计算，让不同版本的 Sigmoid 核函数都能通过统一的接口被 Python 调用，还能适配不同形状的张量，兼顾正确性和效率。

// 定义Sigmoid函数的通用绑定宏，用于批量生成不同版本的C++接口函数
// 参数说明：
//   packed_type：函数名后缀（如f32、f32x4、f16x8，区分不同精度/优化版本）
//   th_type：输入/输出张量要求的PyTorch数据类型（如torch::kFloat32、torch::kHalf）
//   element_type：底层数据类型（如float、half，用于指针转换）
//   n_elements：每个线程处理的元素数量（如1、4、8，匹配对应核函数的优化方式）
#define TORCH_BINDING_SIGMOID(packed_type, th_type, element_type, n_elements)  \
  // 生成具体的Sigmoid接口函数，函数名格式为sigmoid_+packed_type（如sigmoid_f32）
  // 输入x为待计算的PyTorch张量，输出y为存储结果的PyTorch张量（原地计算）
  void sigmoid_##packed_type(torch::Tensor x, torch::Tensor y) {               \
    // 检查输入张量x和输出张量y的数据类型是否符合要求（如是否为float32），不匹配则抛错
    CHECK_TORCH_TENSOR_DTYPE(x, (th_type))                                     \
    CHECK_TORCH_TENSOR_DTYPE(y, (th_type))                                     \
    // 获取输入张量x的维度数量（如2D表示[样本数, 特征数]）
    const int ndim = x.dim();                                                  \
    // 分支1：处理非2维张量（如1D、3D等）
    if (ndim != 2) {                                                           \
      // 计算张量的总元素数N（将各维度大小相乘，如3D张量[2,3,4]的N=2*3*4=24）
      int N = 1;                                                               \
      for (int i = 0; i < ndim; ++i) {                                         \
        N *= x.size(i);                                                        \
      }                                                                        \
      // 配置CUDA线程块大小：256除以每个线程处理的元素数（保证总算力适配256的基准）
      // 如n_elements=4时，块大小=256/4=64
      dim3 block(256 / (n_elements));                                          \
      // 配置CUDA网格大小：向上取整（(N+256-1)/256），确保所有元素都能被处理
      dim3 grid((N + 256 - 1) / 256);                                          \
      // 调用对应的CUDA核函数（如sigmoid_f32_kernel），传入张量的GPU内存指针和总元素数
      sigmoid_##packed_type##_kernel<<<grid, block>>>(                         \
          reinterpret_cast<element_type *>(x.data_ptr()),                      \
          reinterpret_cast<element_type *>(y.data_ptr()), N);                  \
      // 分支2：处理2维张量（最常见场景，如[样本数S, 特征数K]）
    } else {                                                                   \
      // 提取2维张量的两个维度大小：S为样本数，K为每个样本的特征数
      const int S = x.size(0);                                                 \
      const int K = x.size(1);                                                 \
      // 计算总元素数N = 样本数 × 特征数
      const int N = S * K;                                                     \
      // 子分支2.1：若特征数K除以每个线程处理的元素数后≤1024（符合GPU线程块大小限制）
      if ((K / (n_elements)) <= 1024) {                                        \
        // 线程块大小=特征数K / 每个线程处理元素数（让每个线程块处理1个样本的所有特征）
        dim3 block(K / (n_elements));                                          \
        // 网格大小=样本数S（每个网格处理1个样本）
        dim3 grid(S);                                                          \
        // 调用核函数，按“样本级并行”处理2维张量
        sigmoid_##packed_type##_kernel<<<grid, block>>>(                       \
            reinterpret_cast<element_type *>(x.data_ptr()),                    \
            reinterpret_cast<element_type *>(y.data_ptr()), N);                \
        // 子分支2.2：若特征数K过大，超出线程块大小限制（>1024）
      } else {                                                                 \
        // 退化为“总元素数”模式，计算总元素数N
        int N = 1;                                                             \
        for (int i = 0; i < ndim; ++i) {                                       \
          N *= x.size(i);                                                      \
        }                                                                      \
        // 配置线程块和网格大小（同非2维张量的逻辑）
        dim3 block(256 / (n_elements));                                        \
        dim3 grid((N + 256 - 1) / 256);                                        \
        // 调用核函数，按“总元素并行”处理2维张量
        sigmoid_##packed_type##_kernel<<<grid, block>>>(                       \
            reinterpret_cast<element_type *>(x.data_ptr()),                    \
            reinterpret_cast<element_type *>(y.data_ptr()), N);                \
      }                                                                        \
    }                                                                          \
  }

  最后代码通过宏调用批量生成了 6 个不同版本的 Sigmoid 接口函数（涵盖单精度、半精度，以及不同元素并行处理的优化版本），并将这些函数绑定到 PyTorch 扩展模块中。这样一来，Python 代码就能直接调用这些函数，无需关心底层 CUDA 核函数的实现细节，轻松使用不同精度和优化方式的 GPU 加速 Sigmoid 计算，方便对比性能和正确性。

// 调用TORCH_BINDING_SIGMOID宏，生成6个不同版本的Sigmoid接口函数：
// 1. f32版本：单精度浮点（FP32），每个线程处理1个元素
TORCH_BINDING_SIGMOID(f32, torch::kFloat32, float, 1)
// 2. f32x4版本：FP32，每个线程处理4个元素（向量优化）
TORCH_BINDING_SIGMOID(f32x4, torch::kFloat32, float, 4)
// 3. f16版本：半精度浮点（FP16），每个线程处理1个元素
TORCH_BINDING_SIGMOID(f16, torch::kHalf, half, 1)
// 4. f16x2版本：FP16，每个线程处理2个元素（向量优化）
TORCH_BINDING_SIGMOID(f16x2, torch::kHalf, half, 2)
// 5. f16x8版本：FP16，每个线程处理8个元素（向量优化，拆分加载/存储）
TORCH_BINDING_SIGMOID(f16x8, torch::kHalf, half, 8)
// 6. f16x8_pack版本：FP16，每个线程处理8个元素（向量优化，128位打包加载/存储）
TORCH_BINDING_SIGMOID(f16x8_pack, torch::kHalf, half, 8)

// 定义PyTorch扩展模块，模块名由TORCH_EXTENSION_NAME指定（编译时配置，如"sigmoid_lib"）
PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
  // 将生成的6个Sigmoid接口函数绑定到模块m中，使Python可调用：
  // 绑定后，Python中可通过"模块名.sigmoid_f32"等方式调用
  TORCH_BINDING_COMMON_EXTENSION(sigmoid_f32)
  TORCH_BINDING_COMMON_EXTENSION(sigmoid_f32x4)
  TORCH_BINDING_COMMON_EXTENSION(sigmoid_f16)
  TORCH_BINDING_COMMON_EXTENSION(sigmoid_f16x2)
  TORCH_BINDING_COMMON_EXTENSION(sigmoid_f16x8)
  TORCH_BINDING_COMMON_EXTENSION(sigmoid_f16x8_pack)
}

⛪️ 三、小结

⭐️⭐️⭐️ 路漫漫其修远兮，吾将上下而求索。Fighting！⭐️⭐️⭐️