【昇腾CANN训练营·行业篇】渲染未来：基于Ascend C实现高性能3D GridSampler插值算子

2025昇腾CANN训练营推出3D体素采样算子开发实战课程，详解三线性插值(Trilinear)算法在Ascend AI Core的高效实现。课程重点解决3D采样中8点随机访存瓶颈，提出分块加载、权重优化等加速策略，并揭示FP32精度在坐标计算中的关键作用。通过AscendC向量化编程，开发者可掌握NeRF渲染和医学影像处理的核心算子开发技能。完成课程可获得AscendC中级认证及华为设备奖励，报

一行袋码

565人浏览 · 2025-12-09 23:42:09

一行袋码 · 2025-12-09 23:42:09 发布

训练营简介 2025年昇腾CANN训练营第二季，基于CANN开源开放全场景，推出0基础入门系列、码力全开特辑、开发者案例等专题课程，助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证，即可领取精美证书，完成社区任务更有机会赢取华为手机，平板、开发板等大奖。

报名链接：https://www.hiascend.com/developer/activities/cann20252#cann-camp-2502-intro

前言

在 2D 图像处理中，Resize 是最常见的操作，它底层依赖双线性插值（Bilinear）。到了 3D 世界（如医学影像 CT 处理、NeRF 渲染），我们需要在 $D \times H \times W$ 的体积数据中，根据 $(x, y, z)$ 坐标采样出一个值。

这个算子的痛点在于：

访存离散：一个浮点坐标 $(1.5, 2.5, 3.5)$ 涉及到周围 8 个整数坐标的访存。
计算密集：拿到 8 个值后，需要进行 7 次插值运算（x轴3次，y轴2次，z轴1次，或者直接公式计算）。
坐标变换：涉及 align_corners 等繁琐的坐标归一化逻辑。

如果用 Python 写循环，速度慢到无法接受。在 Ascend AI Core 上，我们可以利用 Vector 单元的强大算力 配合 Gather 机制，实现并行的体素采样。

一、核心图解：捕捉空间中的幽灵点

GridSample 的本质是：用已知的离散点，去猜测未知的连续点。

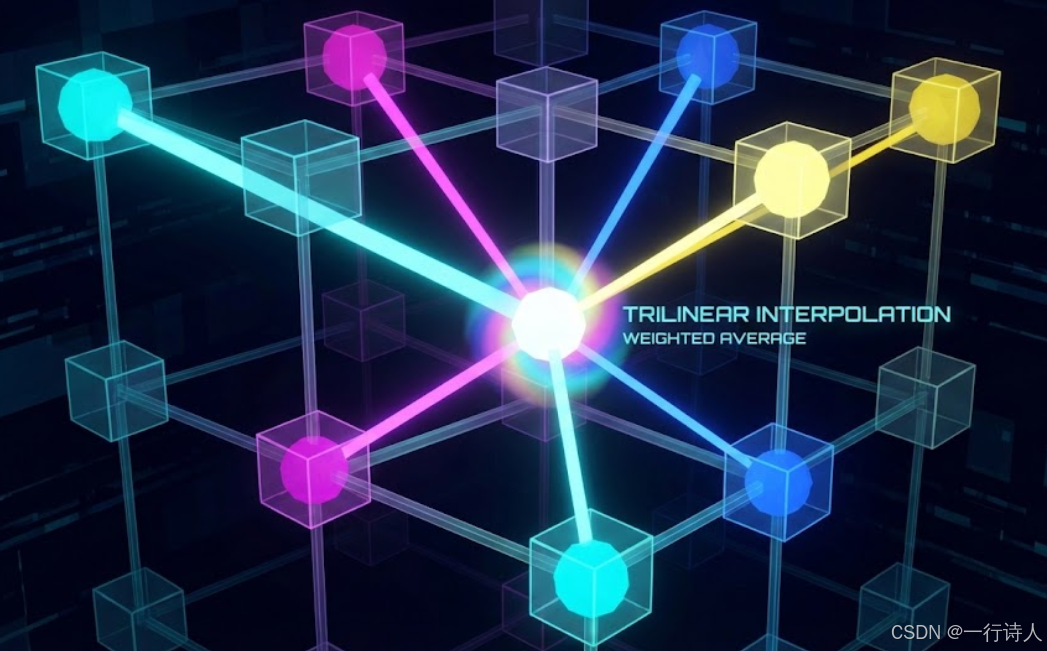
二、算法原理：三线性插值 (Trilinear)

假设输入 Grid 大小为 $D \times H \times W$，查询坐标为 $(x, y, z)$（已归一化到像素坐标系）。

定位：计算左上角整数坐标 $(x_0, y_0, z_0) = (\lfloor x \rfloor, \lfloor y \rfloor, \lfloor z \rfloor)$。
权重：计算距离权重 $\alpha = x - x_0, \beta = y - y_0, \gamma = z - z_0$。
取值：获取周围 8 个顶点的值 $V_{000} \dots V_{111}$。
- $V_{000} = \text{Grid}[z_0, y_0, x_0]$
- ...
- $V_{111} = \text{Grid}[z_0+1, y_0+1, x_0+1]$
混合：公式如下：
$$\begin{aligned} V_{xyz} &= (1-\alpha)(1-\beta)(1-\gamma)V_{000} + \alpha(1-\beta)(1-\gamma)V_{100} \\ &+ (1-\alpha)\beta(1-\gamma)V_{010} + \dots + \alpha\beta\gamma V_{111} \end{aligned}$$

三、实战：Ascend C 实现

我们的目标是并行处理 $N$ 个采样点。

3.1 Kernel 类定义

输入：grid $[D, H, W, C]$，grid_coords $[N, 1, 1, 3]$。输出：output $[N, 1, 1, C]$。

class KernelGridSampler3D {
public:
    __aicore__ inline void Init(GM_ADDR grid, GM_ADDR coords, GM_ADDR output, 
                                uint32_t num_points, uint32_t c_dim, 
                                uint32_t d, uint32_t h, uint32_t w) {
        // ... Init ...
        // 保存 Grid 维度信息用于坐标计算
        this->depth = d; this->height = h; this->width = w;
        this->channel = c_dim;
    }
    
    __aicore__ inline void Process() {
        // Tiling: 按采样点数量 N 切分
        for (int i = 0; i < tileNum; i++) {
            Compute(i);
        }
    }
};

3.2 Compute 核心逻辑

__aicore__ inline void Compute(int32_t i) {
    // 1. 搬运坐标到 UB
    // coordsLoc: [tileLen, 3] (x, y, z)
    DataCopy(coordsLoc, coordsGm[offset], tileLen * 3);

    // 2. 坐标反归一化 (Normalize -> Pixel)
    // 假设输入是 [-1, 1]，转为 [0, W-1]
    // pixel_x = ((x + 1) / 2) * (W - 1)
    // 这一步全是 Vector 计算 (Adds, Muls)
    ComputePixelCoords(coordsLoc);

    // 3. 计算 8 个角点的坐标 (Integer Index)
    // floor_x, ceil_x 等
    // 还要处理边界 Padding (Clamp 到 0~W-1)
    // 结果存入 idx000, idx001 ... idx111 (共 8 个 index tensor)
    
    // 4. 计算插值权重 (Float Weight)
    // alpha = x - floor_x
    // beta  = y - floor_y
    // gamma = z - floor_z
    // 预计算 8 个混合系数: w000 = (1-a)(1-b)(1-c) ...
    
    // 5. Gather (最耗时步骤)
    // 这里的 Grid 通常很大，在 GM 里。我们用 Gather 抓取 8 次。
    // 注意：如果是多 Channel，每个采样点要抓 C 个数。
    // 最好把 Grid reshape 成 [D*H*W, C]，然后 Gather 索引为 (z*H*W + y*W + x)
    
    for (int k = 0; k < 8; k++) {
        // 根据 idx 计算线性偏移 linear_idx
        // Gather(val_k, gridGm, linear_idx, ...)
        // 这一步会产生大量的随机访存，是性能瓶颈
    }

    // 6. 加权求和 (FMA)
    // out = val_000 * w000 + val_001 * w001 + ...
    Muls(outLoc, val_000, w000, tileLen * channel);
    Mad(outLoc, val_001, w001, tileLen * channel);
    // ... 重复 8 次累加 ...

    // 7. CopyOut
    DataCopy(outGm, outLoc, ...);
}

四、性能优化的“神来之笔”

3D GridSample 的瓶颈在于 Gather 次数太多（每个点要读 8 次内存）。

4.1 局部性优化：Block Loading

如果采样点是空间连续的（例如渲染一张完整的图），那么相邻的采样点很可能共享同一个 Voxel。优化：不要一个个点 Gather。先把 Grid 的一个小块（例如 $4 \times 4 \times 4$）搬到 UB，然后让落在该区域内的所有采样点直接在 UB 查表。这需要 Host 侧对采样点进行空间排序 (Spatial Sorting)。